
���}Ŀ���x��4-4������(bi��o)ϵ�c����(sh��)����
��ƽ��ֱ������(bi��o)ϵ![]() ��ֱ��
��ֱ��![]() �ăAб�Ǟ�
�ăAб�Ǟ�![]() ���ҽ�(j��ng)�^�c(di��n)
���ҽ�(j��ng)�^�c(di��n)![]() ��������(bi��o)ϵ
��������(bi��o)ϵ![]() ��ԭ�c(di��n)��O�c(di��n)��
��ԭ�c(di��n)��O�c(di��n)�� ![]() �S�ķ�ؓ(f��)���S��O�S�������O����(bi��o)ϵ
�S�ķ�ؓ(f��)���S��O�S�������O����(bi��o)ϵ![]() ������
������![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ��ֱ��
��ֱ��![]() �c����
�c����![]() �ཻ��
�ཻ��![]() ���c(di��n)���^�c(di��n)
���c(di��n)���^�c(di��n)![]() ��ֱ��
��ֱ��![]() �c����
�c����![]() �ཻ��
�ཻ��![]() ���c(di��n)����
���c(di��n)����![]() ��
��
��1��ƽ��ֱ������(bi��o)ϵ�У���ֱ��![]() ��һ�㷽�̺�����
��һ�㷽�̺�����![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2�����C�� ![]() �鶨ֵ��
�鶨ֵ��
���𰸡���1��![]() ,
,![]() ��2��
��2��![]()
��������ԇ�}��������1������(j��)�c(di��n)бʽ�ɵ�ֱ��![]() ��һ�㷽�̣�ע��ӑՓб�ʲ����ڵ����Σ�����(j��)
��һ�㷽�̣�ע��ӑՓб�ʲ����ڵ����Σ�����(j��)![]() ������
������![]() �ĘO����(bi��o)���̻���ֱ������(bi��o)���̣��䷽�����(bi��o)��(zh��n)����.��2������ֱ������(sh��)���̎����x�����L�����г�ֱ������(sh��)���̣�����A���̣�����(j��)
�ĘO����(bi��o)���̻���ֱ������(bi��o)���̣��䷽�����(bi��o)��(zh��n)����.��2������ֱ������(sh��)���̎����x�����L�����г�ֱ������(sh��)���̣�����A���̣�����(j��)![]() ���f�_(d��)�����ɵ�
���f�_(d��)�����ɵ�![]() ����ƿɵ�
����ƿɵ�![]() ����Ӽ��ýY(ji��)Փ.
����Ӽ��ýY(ji��)Փ.
ԇ�}�������⣺��1����?y��n)�ֱ��![]() �ăAб�Ǟ�
�ăAб�Ǟ�![]() ���ҽ�(j��ng)�^�c(di��n)
���ҽ�(j��ng)�^�c(di��n)![]() ��
��
��(d��ng)![]() �r(sh��)��ֱ��
�r(sh��)��ֱ��![]() ��ֱ��
��ֱ��![]() �S��������һ�㷽�̞�
�S��������һ�㷽�̞�![]() ��
��
��(d��ng)![]() �r(sh��)��ֱ��
�r(sh��)��ֱ��![]() ��б�ʞ�
��б�ʞ�![]() �������䷽�̞�
�������䷽�̞�![]() ��
��
��һ�㷽�̞�![]() ��
��
��?y��n)?/span>![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ������
������![]() ��
��
��?y��n)?/span>![]() ������
������![]() ��
��
��������![]() �Ę�(bi��o)��(zh��n)���̞�
�Ę�(bi��o)��(zh��n)���̞�![]() ��
��
��2���O(sh��)ֱ��![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)����
�酢��(sh��)����
��������![]() �Ę�(bi��o)��(zh��n)���̞�
�Ę�(bi��o)��(zh��n)���̞�![]() ��
��
�ɵ�![]() ����
����![]() ��
��
�t![]() ��
��
����![]() ��
��
ͬ��![]() ��
��
����![]() ��
��



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���x��4-4������(bi��o)ϵ�c����(sh��)����
��ֱ������(bi��o)ϵ![]() �У���֪�c(di��n)
�У���֪�c(di��n)![]() ������
������![]() �ą���(sh��)���̞�
�ą���(sh��)���̞� ��
��![]() �酢��(sh��)������ԭ�c(di��n)��O�c(di��n)��
�酢��(sh��)������ԭ�c(di��n)��O�c(di��n)�� ![]() �S�����S��O�S�����O����(bi��o)ϵ��ֱ��
�S�����S��O�S�����O����(bi��o)ϵ��ֱ��![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞� ��
��
�����Д��c(di��n)![]() �cֱ��
�cֱ��![]() ��λ���P(gu��n)ϵ���f�����ɣ�
��λ���P(gu��n)ϵ���f�����ɣ�
�����O(sh��)ֱ��![]() �c����
�c����![]() �ăɂ�(g��)���c(di��n)�քe��
�ăɂ�(g��)���c(di��n)�քe��![]() ��
�� ![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������ĽM����(sh��)�У���ͬһ��(g��)����(sh��)���ǣ� ��
A.![]() ��
�� ![]()
B.f��x��=2log2x�� ![]()
C.f��x��=ln��x��1����ln��x+1���� ![]()
D.f��x��=lg��1��x��+lg��1+x����g��x��=lg��1��x2��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������(sh��)f��x��=loga��x+1������a��0��a��1���ĈD��(j��ng)�^�c(di��n)���� ![]() ����2�����D����������(g��)�c(di��n)A��B��C�������ęM����(bi��o)���Ξ�t��1��t��t+1����t��1����ӛ������ABC����e��S��t����
����2�����D����������(g��)�c(di��n)A��B��C�������ęM����(bi��o)���Ξ�t��1��t��t+1����t��1����ӛ������ABC����e��S��t���� 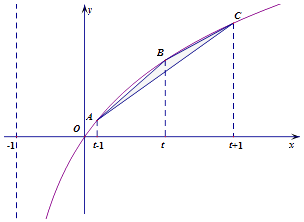
��1����f��x���ı��_(d��)ʽ��
��2����S��1����
��3���Ƿ����������(sh��)m��ʹ�Ì���һ�в�С��1��t������S��t����m�������������Сֵ���������ڣ�Ո�f�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�AC�� ![]() ��a��b��0���^�c(di��n)P����1����1����c��E�A�İ뽹�࣬��c=
��a��b��0���^�c(di��n)P����1����1����c��E�A�İ뽹�࣬��c= ![]() b���^�c(di��n)P���ɗl���ഹֱ��ֱ��l1 �� l2�c�E�AC�քe��������c(di��n)M��N��
b���^�c(di��n)P���ɗl���ഹֱ��ֱ��l1 �� l2�c�E�AC�քe��������c(di��n)M��N��
��1����E�AC�ķ��̣�
��2����ֱ��l1��б�ʞ驁1�����PMN����e��
��3��������MN�����c(di��n)��x�S�ϣ���ֱ��MN�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�纯��(sh��)y=x3m��9��m��N*���ĈD���P(gu��n)��y�S���Q�����ڣ�0��+�ޣ��Ϻ���(sh��)ֵ�Sx������pС��
��1����m��ֵ��
��2����M�㣨a+1�� ![]() ����3��2a��
����3��2a�� ![]() ��a�ķ�����
��a�ķ�����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���x��?y��n)�R�ĺ���(sh��)f��x��= ![]() ���溯��(sh��)��
���溯��(sh��)��
��1����a��b��ֵ��
��2���Дຯ��(sh��)�Ć��{(di��o)�Բ��C����
��3���������t��R������ʽf��t2��2t��+f��2t2��k����0���������k��ȡֵ������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪P����2��3���Ǻ���(sh��)y= ![]() �D���ϵ��c(di��n)��Q���p�����ڵ��������@һ��֧�ϵĄ��c(di��n)���^�c(di��n)Q��ֱ����ʹ���c�p����y=
�D���ϵ��c(di��n)��Q���p�����ڵ��������@һ��֧�ϵĄ��c(di��n)���^�c(di��n)Q��ֱ����ʹ���c�p����y= ![]() ֻ��һ��(g��)�����c(di��n)�����cx�S��y�S�քe�����c(di��n)C��D����һ�lֱ��y=
ֻ��һ��(g��)�����c(di��n)�����cx�S��y�S�քe�����c(di��n)C��D����һ�lֱ��y= ![]() x+6�cx�S��y�S�քe�����c(di��n)A��B���t
x+6�cx�S��y�S�քe�����c(di��n)A��B���t
��1��O������(bi��o)ԭ�c(di��n)��������OCD����e�� ��
��2����߅��ABCD��e����Сֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�P(gu��n)��x�IJ���ʽ��|2x��m|��1������(sh��)�����҃H��һ��(g��)ֵ��2��
��1��������(sh��)m��ֵ��
��2���ڣ�1���ėl���£��ⲻ��ʽ��|x��1|+|x��3|��m��
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com