已知函數(shù)
.
(1)求函數(shù)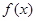
的最小正周期和圖像的對稱軸方程；
(2)求函數(shù)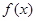在區(qū)間
上的值域.
（1）
，
；（2）
解析試題分析：（1）先利用兩角和與差的三角函數(shù)將式子展開合并，再利用二倍角公式、輔助角公式化簡得到
，再結(jié)合正弦函數(shù)的性質(zhì)，由
、
可得函數(shù)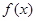的最小正周期與對稱軸的方程；（2）將
當成整體，由
，利用正弦函數(shù)的單調(diào)性可得
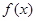，即的值域.
試題解析：（1）
所以函數(shù)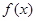的周期
由
，得
所以函數(shù)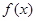圖像的對稱軸方程為 6分
（2）因為
，所以
因為在區(qū)間
上單調(diào)遞增，在區(qū)間
上單調(diào)遞減
所以當
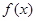時，取最大值1
又因為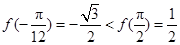
，當
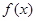時，取最小值
所以函數(shù)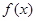在區(qū)間
上的值域為 10分.
考點：1.三角函數(shù)的圖像與性質(zhì)；2.三角恒等變換.
沖刺100分單元優(yōu)化練考卷系列答案科目：高中數(shù)學(xué) 來源： 題型：解答題
已知f(x)=Asin(ωx+φ)(A>0,ω>0)的最小正周期為2,且當x=
時,f(x)的最大值為2.
(1)求f(x)的解析式.
(2)在閉區(qū)間[
,
]上是否存在f(x)的對稱軸?如果存在求出其對稱軸.若不存在,請說明理由.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
已知函數(shù)
.
（1）請用“五點法”畫出函數(shù)
在長度為一個周期的閉區(qū)間上的簡圖（先在所給的表格中填上所需的數(shù)值，再畫圖）；
| | | | | | |
| | | | | | |
| | | | | | |
的單調(diào)遞增區(qū)間；
時，求函數(shù)的最大值和最小值及相應(yīng)的
的值.查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
已知函數(shù)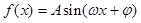
（其中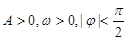
）的部分圖象如圖所示．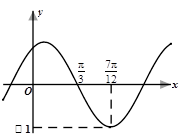
（1）求函數(shù)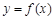
的解析式；
（2）求函數(shù)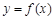的單調(diào)增區(qū)間；
（3）求方程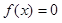
的解集．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：解答題
已知向量a=
，b=
，設(shè)函數(shù)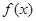
=a
b．
（Ⅰ）求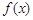
的單調(diào)遞增區(qū)間；
（Ⅱ）若將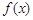的圖象向左平移
個單位，得到函數(shù)
的圖象，求函數(shù)在區(qū)間
上的最大值和最小值．
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的值；
的值；
是第三象限角，求
的值.
．
的值；
在區(qū)間
上的最大值和最小值．
中,已知
.
; 
求角A的大小.
中,三個內(nèi)角
所對的邊分別為
已知
，
.
；
求
的值.