
【題目】已知正數(shù)數(shù)列![]() 的前n項和為
的前n項和為![]() ,滿足
,滿足![]() ,
,![]() .
.
(1)求數(shù)列![]() 的通項公式,若
的通項公式,若![]() 恒成立,求k的范圍;
恒成立,求k的范圍;
(2)設(shè)![]() ,若
,若![]() 是遞增數(shù)列,求實數(shù)a的取值范圍.
是遞增數(shù)列,求實數(shù)a的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由![]() ,得
,得![]() =Sn﹣1+Sn﹣2,(n≥3).相減可得:
=Sn﹣1+Sn﹣2,(n≥3).相減可得:![]() =an+an﹣1,(n≥3),根據(jù)an>0,可得an﹣an﹣1=1(n≥3),當(dāng)n=2時,
=an+an﹣1,(n≥3),根據(jù)an>0,可得an﹣an﹣1=1(n≥3),當(dāng)n=2時,![]() =a1+a2+a1,解得
=a1+a2+a1,解得![]() ,進(jìn)而得出an,利用裂項相消法化簡
,進(jìn)而得出an,利用裂項相消法化簡![]() 恒成立,從而求出k的范圍;
恒成立,從而求出k的范圍;
(2)由(1)得![]() (n﹣1)2+a(n﹣1),利用
(n﹣1)2+a(n﹣1),利用![]() 是遞增數(shù)列,可得bn+1﹣bn>0恒成立,即可實數(shù)a的取值范圍.
是遞增數(shù)列,可得bn+1﹣bn>0恒成立,即可實數(shù)a的取值范圍.
(1)由![]() ,得
,得![]() =Sn-1+Sn﹣2,(n≥3).相減可得:
=Sn-1+Sn﹣2,(n≥3).相減可得:![]() =an+an﹣1(n≥3),
=an+an﹣1(n≥3),
∵an>0,∴an﹣1>0,∴平方差公式化簡得an﹣an﹣1=1,(n≥3).
當(dāng)n=2時,![]() =a1+a2+a1,且
=a1+a2+a1,且![]() ,∴
,∴![]() =2+
=2+![]() ,
,![]() >0,∴
>0,∴![]() =2或
=2或![]() =-1.因此當(dāng)n=2時,an﹣an﹣1=1成立.
=-1.因此當(dāng)n=2時,an﹣an﹣1=1成立.
∴數(shù)列{an}是以![]() 為首項,以1為公差的等差數(shù)列,∴an=1+n﹣1=n.
為首項,以1為公差的等差數(shù)列,∴an=1+n﹣1=n.
![]()
![]()
由題意得,k![]() .
.
(2)由(1)得,![]() =(n﹣1)2+a(n﹣1),
=(n﹣1)2+a(n﹣1),
∵![]() 是遞增數(shù)列,∴bn+1﹣bn=n2+an﹣(n﹣1)2﹣a(n﹣1)=2n+a﹣1>0,
是遞增數(shù)列,∴bn+1﹣bn=n2+an﹣(n﹣1)2﹣a(n﹣1)=2n+a﹣1>0,
即![]() 恒成立,∵
恒成立,∵![]() ,∴a
,∴a![]() ﹣1,∴實數(shù)a的取值范圍是
﹣1,∴實數(shù)a的取值范圍是![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() (
(![]() 為參數(shù)),A,B是C上的動點,且滿足
為參數(shù)),A,B是C上的動點,且滿足![]() (O為坐標(biāo)原點),以原點O為極點,x軸的正半軸為極軸建立坐標(biāo)系,點D的極坐標(biāo)為
(O為坐標(biāo)原點),以原點O為極點,x軸的正半軸為極軸建立坐標(biāo)系,點D的極坐標(biāo)為![]() .
.
(1)求橢圓C的極坐標(biāo)方程和點D的直角坐標(biāo);
(2)利用橢圓C的極坐標(biāo)方程證明 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】一汽車廠生產(chǎn)A,B,C三類轎車,每類轎車均有舒適型和標(biāo)準(zhǔn)型兩種型號,某月的產(chǎn)量如表所示(單位輛),若按A,B,C三類用分層抽樣的方法在這個月生產(chǎn)的轎車中抽取50輛,則A類轎車有10輛
轎車A | 轎車B | 轎車C | |
舒適型 | 100 | 150 | z |
標(biāo)準(zhǔn)型 | 300 | 450 | 600 |
(1)求下表中z的值;
(2)用隨機(jī)抽樣的方法從B類舒適型轎車中抽取8輛,經(jīng)檢測它們的得分如下:94,86,92,96,87,93,90,82把這8輛轎車的得分看作一個總體,從中任取一個得分?jǐn)?shù)![]() 記這8輛轎車的得分的平均數(shù)為
記這8輛轎車的得分的平均數(shù)為![]() ,定義事件
,定義事件![]() {
{![]() ,且函數(shù)
,且函數(shù)![]() 沒有零點},求事件
沒有零點},求事件![]() 發(fā)生的概率
發(fā)生的概率
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖:在四棱錐![]() 中,
中,![]() 平面
平面![]() .
.![]() ,
,![]() ,
,![]() .點
.點![]() 是
是![]() 與
與![]() 的交點,點
的交點,點![]() 在線段
在線段![]() 上且
上且![]() .
.

(1)證明:![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的正切值.
的正切值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】有下列說法:
①在殘差圖中,殘差點比較均勻地落在水平的帶狀區(qū)域內(nèi),說明選用的模型比較合適;
②用相關(guān)指數(shù)R2來刻畫回歸的效果,R2值越大,說明模型的擬合效果越好;
③比較兩個模型的擬合效果,可以比較殘差平方和的大小,殘差平方和越小的模型,擬合效果越好.
④在研究氣溫和熱茶銷售杯數(shù)的關(guān)系時,若求得相關(guān)指數(shù)R2≈0.85,則表明氣溫解釋了15%的熱茶銷售杯數(shù)變化.
其中正確命題的個數(shù)是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,函數(shù)
,函數(shù)![]() .
.
(1)若函數(shù)![]() 在
在![]() 上單調(diào)遞增,求a的取值范圍;
上單調(diào)遞增,求a的取值范圍;
(2)用反證法證明:函數(shù)![]() 不可能為
不可能為![]() 上的單調(diào)函數(shù).
上的單調(diào)函數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】統(tǒng)計學(xué)中,經(jīng)常用環(huán)比、同比來進(jìn)行數(shù)據(jù)比較,環(huán)比是指本期統(tǒng)計數(shù)據(jù)與上期比較,如![]() 年
年![]() 月與
月與![]() 年
年![]() 月相比,同比是指本期數(shù)據(jù)與歷史同時期比較,如
月相比,同比是指本期數(shù)據(jù)與歷史同時期比較,如![]() 年
年![]() 月與
月與![]() 年
年![]() 月相比.
月相比.
環(huán)比增長率![]() (本期數(shù)
(本期數(shù)![]() 上期數(shù))
上期數(shù))![]() 上期數(shù)
上期數(shù)![]() ,
,
同比增長率![]() (本期數(shù)
(本期數(shù)![]() 同期數(shù))
同期數(shù))![]() 同期數(shù)
同期數(shù)![]() .
.
下表是某地區(qū)近![]() 個月來的消費者信心指數(shù)的統(tǒng)計數(shù)據(jù):
個月來的消費者信心指數(shù)的統(tǒng)計數(shù)據(jù):
序號 |
|
|
|
|
|
|
|
|
時間 |
|
|
|
|
|
|
|
|
消費者信心指數(shù) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2017年
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() 求該地區(qū)
求該地區(qū)![]() 年
年![]() 月消費者信心指數(shù)的同比增長率(百分比形式下保留整數(shù));
月消費者信心指數(shù)的同比增長率(百分比形式下保留整數(shù));
![]() 除
除![]() 年
年![]() 月以外,該地區(qū)消費者信心指數(shù)月環(huán)比增長率為負(fù)數(shù)的有幾個月?
月以外,該地區(qū)消費者信心指數(shù)月環(huán)比增長率為負(fù)數(shù)的有幾個月?
![]() 由以上數(shù)據(jù)可判斷,序號
由以上數(shù)據(jù)可判斷,序號![]() 與該地區(qū)消費者信心指數(shù)
與該地區(qū)消費者信心指數(shù)![]() 具有線性相關(guān)關(guān)系,寫出
具有線性相關(guān)關(guān)系,寫出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() (
(![]() ,
,![]() 保留
保留![]() 位小數(shù)),并依此預(yù)測該地區(qū)
位小數(shù)),并依此預(yù)測該地區(qū)![]() 年
年![]() 月的消費者信心指數(shù)(結(jié)果保留
月的消費者信心指數(shù)(結(jié)果保留![]() 位小數(shù),參考數(shù)據(jù)與公式:
位小數(shù),參考數(shù)據(jù)與公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
, )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
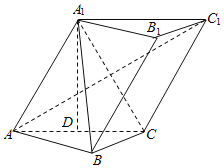
【題目】如圖,三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=A1C=2,平面ACC1A1⊥平面ABC.現(xiàn)以邊AC的中點D為坐標(biāo)原點,平面ABC內(nèi)垂直于AC的直線為![]() 軸,直線AC為
軸,直線AC為![]() 軸,直線DA1為
軸,直線DA1為![]() 軸建立空間直角坐標(biāo)系,解決以下問題:
軸建立空間直角坐標(biāo)系,解決以下問題:
(1)求異面直線AB與A1C所成角的余弦值;
(2)求直線AB與平面A1BC所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖兩個同心球,球心均為點![]() ,其中大球與小球的表面積之比為3:1,線段
,其中大球與小球的表面積之比為3:1,線段![]() 與
與![]() 是夾在兩個球體之間的內(nèi)弦,其中
是夾在兩個球體之間的內(nèi)弦,其中![]() 兩點在小球上,
兩點在小球上,![]() 兩點在大球上,兩內(nèi)弦均不穿過小球內(nèi)部.當(dāng)四面體
兩點在大球上,兩內(nèi)弦均不穿過小球內(nèi)部.當(dāng)四面體![]() 的體積達(dá)到最大值時,此時異面直線
的體積達(dá)到最大值時,此時異面直線![]() 與
與![]() 的夾角為
的夾角為![]() ,則
,則![]() ( )
( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com