
【題目】已知![]() .
.
(1)當(dāng)![]() 時,求
時,求![]() 的值域;
的值域;
(2)若b為正實數(shù),![]() 的最大值為M,最小值為m,且滿足
的最大值為M,最小值為m,且滿足![]() ,求b的取值范圍.
,求b的取值范圍.
【答案】見解析
【解析】(1)當(dāng)![]() 時,
時,![]() .
.
因為![]() 在[1,
在[1,![]() ]上單調(diào)遞減,在[
]上單調(diào)遞減,在[![]() ,2]上單調(diào)遞增,
,2]上單調(diào)遞增,
所以![]() 的最小值為
的最小值為![]() .
.
又![]() ,所以
,所以![]() 的值域為[
的值域為[![]() ,0].
,0].
(2)①當(dāng)0<b<2時,![]() 在[1,2]上單調(diào)遞增,
在[1,2]上單調(diào)遞增,
則![]() ,M=
,M=![]() -1,
-1,
此時M-m=-![]() +1≥4,得b≤-6,與0<b<2矛盾,舍去;
+1≥4,得b≤-6,與0<b<2矛盾,舍去;
②當(dāng)2≤b<4時,![]() 在[1,
在[1,![]() ]上單調(diào)遞減,在[
]上單調(diào)遞減,在[![]() ,2]上單調(diào)遞增,
,2]上單調(diào)遞增,
所以![]() ,
,![]() ,則
,則 ![]() ,得(
,得(![]() -1)2≥4,解得b≥9,與2≤b<4矛盾,舍去;
-1)2≥4,解得b≥9,與2≤b<4矛盾,舍去;
③當(dāng)b≥4時,![]() 在[1,2]上單調(diào)遞減,
在[1,2]上單調(diào)遞減,
則M=b-2,m=![]() -1,此時M-m=
-1,此時M-m=![]() -1≥4,得b≥10.
-1≥4,得b≥10.
綜上所述,b的取值范圍是[10,+∞).


 口算題卡加應(yīng)用題集訓(xùn)系列答案
口算題卡加應(yīng)用題集訓(xùn)系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】十八屆五種全會公報指出:努力促進人口均衡發(fā)展,堅持計劃生育的基本國策,完善人口發(fā)展戰(zhàn)略,全面實施一對夫婦可生育兩個孩子的政策,提高生殖保健、婦幼保健、托兒等公共服務(wù)水平.為了解適齡公務(wù)員對放開生育二胎政策的態(tài)度,某部門隨機調(diào)查了100位30到40歲的公務(wù)員,得到情況如下表:
男公務(wù)員 | 女公務(wù)員 | |
生二胎 | 40 | 20 |
不生二胎 | 20 | 20 |
(1)是否有95%以上的把握認為“生二胎與性別有關(guān)”,并說明理由;
(2)把以上頻率當(dāng)概率,若從社會上隨機抽取3位30到40歲的男公務(wù)員,記其中生二胎的人數(shù)為![]() ,求隨機變量
,求隨機變量![]() 的分布列,數(shù)學(xué)期望.
的分布列,數(shù)學(xué)期望.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
附:![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在直角坐標系![]() 中,曲線
中,曲線![]() ,曲線
,曲線![]() 為參數(shù)), 以坐標原點
為參數(shù)), 以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)若射線![]() 分別交
分別交![]() 于
于![]() 兩點, 求
兩點, 求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)設(shè)![]() ,
,
①記![]() 的導(dǎo)函數(shù)為
的導(dǎo)函數(shù)為![]() ,求
,求![]() ;
;
②若方程![]() 有兩個不同實根,求實數(shù)
有兩個不同實根,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若在![]() 上存在一點
上存在一點![]() 使
使![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() 在
在![]() 處取最小值.
處取最小值.
(1)求![]() 的值,并化簡
的值,并化簡 ![]() ;
;
(2)在![]() ABC中,
ABC中,![]() 分別是角A,B, C的對邊,已知
分別是角A,B, C的對邊,已知![]()
![]() ,求角C.
,求角C.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知{an}是等差數(shù)列,{bn}是等比數(shù)列,且b2=3,b3=9,a1=b1,a14=b4.
(1)求{an}的通項公式;
(2)設(shè)cn=an+bn,求數(shù)列{cn}的前n項和.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知過點A(0,1)且斜率為k的直線l與圓C:(x-2)2+(y-3)2=1交于M,N兩點.
(1)求k的取值范圍;
(2)若![]() =12,其中O為坐標原點,求|MN|.
=12,其中O為坐標原點,求|MN|.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標系中,以原點為極點,x軸的正半軸為極軸建立極坐標系,已知曲線C:ρsin2θ=2acos θ(a>0),過點P(-2,-4)的直線l: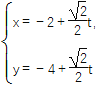 (t為參數(shù))與曲線C相交于M,N兩點.
(t為參數(shù))與曲線C相交于M,N兩點.
(1)求曲線C的直角坐標方程和直線l的普通方程;
(2)若|PM|,|MN|,|PN|成等比數(shù)列,求實數(shù)a的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com