
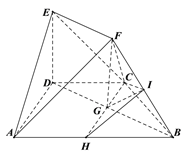
【題目】如圖,在四邊形ABCD中,AB//CD,∠ABD=30°,AB=2CD=2AD=2,DE⊥平面ABCD,EF//BD,且BD=2EF.
(Ⅰ)求證:平面ADE⊥平面BDEF;
(Ⅱ)若二面角C![]() BF
BF![]() D的大小為60°,求CF與平面ABCD所成角的正弦值.
D的大小為60°,求CF與平面ABCD所成角的正弦值.

【答案】(1)見解析(2)![]()
【解析】分析:(1)根據面面垂直的判定定理即可證明平面ADE⊥平面BDEF;
(2)建立空間直角坐標系,利用空間向量法即可求CF與平面ABCD所成角的正弦值;也可以應用常規法,作出線面角,放在三角形當中來求解.
詳解:(Ⅰ)在△ABD中,∠ABD=30°,由AO2=AB2+BD2-2AB·BDcos30°,
解得BD=![]() ,所以AB2+BD2=AB2,根據勾股定理得∠ADB=90°∴AD⊥BD.
,所以AB2+BD2=AB2,根據勾股定理得∠ADB=90°∴AD⊥BD.
又因為DE⊥平面ABCD,AD![]() 平面ABCD,∴AD⊥DE.
平面ABCD,∴AD⊥DE.
又因為BD![]() DE=D,所以AD⊥平面BDEF,又AD
DE=D,所以AD⊥平面BDEF,又AD![]() 平面ABCD,
平面ABCD,
∴平面ADE⊥平面BDEF,
(Ⅱ)方法一:
如圖,由已知可得![]() ,
,![]() ,則
,則
![]() ,則三角形BCD為銳角為30°的等腰三角形.
,則三角形BCD為銳角為30°的等腰三角形.
![]() 則
則![]() .
.
過點C做![]() ,交DB、AB于點G,H,則點G為點F在面ABCD上的投影.連接FG,則
,交DB、AB于點G,H,則點G為點F在面ABCD上的投影.連接FG,則
![]() ,DE⊥平面ABCD,則
,DE⊥平面ABCD,則![]() 平面
平面![]() .
.
過G做![]() 于點I,則BF
于點I,則BF![]() 平面
平面![]() ,即角
,即角![]() 為
為
二面角C![]() BF
BF![]() D的平面角,則
D的平面角,則![]() 60°.
60°.
則![]() ,
,![]() ,則
,則![]() .
.
在直角梯形BDEF中,G為BD中點,![]() ,
,![]() ,
,![]() ,
,
設![]() ,則
,則![]() ,
,![]() ,則
,則![]() .
.
![]() ,則
,則![]() ,即CF與平面ABCD所成角的正弦值為
,即CF與平面ABCD所成角的正弦值為![]() .
.
(Ⅱ)方法二:
 可知DA、DB、DE兩兩垂直,以D為原點,建立如圖所示的空間直角坐標系D-xyz.
可知DA、DB、DE兩兩垂直,以D為原點,建立如圖所示的空間直角坐標系D-xyz.
設DE=h,則D(0,0,0),B(0,![]() ,0),C(-
,0),C(-![]() ,-
,-![]() ,h).
,h).
![]() ,
,![]() .
.
設平面BCF的法向量為m=(x,y,z),
則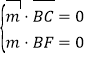 所以
所以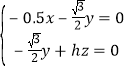 取x=
取x=![]() ,所以m=(
,所以m=(![]() ,-1
,-1![]() ),
),
取平面BDEF的法向量為n=(1,0,0),
由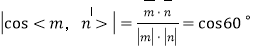 ,解得
,解得![]() ,則
,則![]() ,
,
又![]() ,則
,則![]() ,設CF與平面ABCD所成角為
,設CF與平面ABCD所成角為![]() ,
,
則sin![]() =
=![]() .
.
故直線CF與平面ABCD所成角的正弦值為![]()


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:高中數學 來源: 題型:
【題目】設兩實數![]() 不相等且均不為
不相等且均不為![]() .若函數
.若函數![]() 在
在![]() 時,函數值
時,函數值![]() 的取值區間恰為
的取值區間恰為![]() ,就稱區間
,就稱區間![]() 為
為![]() 的一個“倒域區間”.已知函數
的一個“倒域區間”.已知函數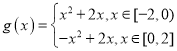 .
.
(1)求函數![]() 在
在![]() 內的“倒域區間”;
內的“倒域區間”;
(2)若函數![]() 在定義域
在定義域![]() 內所有“倒域區間”的圖象作為函數
內所有“倒域區間”的圖象作為函數![]() 的圖象,是否存在實數
的圖象,是否存在實數![]() ,使得
,使得![]() 與
與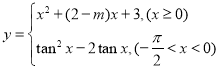 恰好有2個公共點?若存在,求出
恰好有2個公共點?若存在,求出![]() 的取值范圍:若不存在,請說明理由.
的取值范圍:若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據以往的成績記錄,甲、乙兩名隊員射擊中靶環數(環數為整數)的頻率分布情況如圖所示.假設每名隊員每次射擊相互獨立.

(Ⅰ)求圖中a的值;
(Ⅱ)隊員甲進行2次射擊.用頻率估計概率,求甲恰有1次中靶環數大于7的概率;
(Ⅲ)在隊員甲、乙中,哪一名隊員的射擊成績更穩定?(結論無需證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
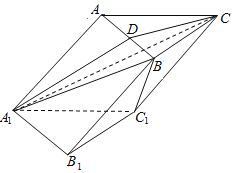
【題目】如圖,在底邊為等邊三角形的斜三棱柱ABC﹣A1B1C1中,AA1![]() AB,四邊形B1C1CB為矩形,過A1C作與直線BC1平行的平面A1CD交AB于點D.
AB,四邊形B1C1CB為矩形,過A1C作與直線BC1平行的平面A1CD交AB于點D.
(Ⅰ)證明:CD⊥AB;
(Ⅱ)若AA1與底面A1B1C1所成角為60°,求二面角B﹣A1C﹣C1的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】利用獨立性檢驗的方法調查高中生的寫作水平與離好閱讀是否有關,隨機詢問120名高中生是否喜好閱讀,利用2×2列聯表,由計算可得K2=4.236
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
參照附表,可得正確的結論是( )
A.有95%的把握認為“寫作水平與喜好閱讀有關”
B.有97.5%的把握認為“寫作水平與喜好閱讀有關”
C.有95%的把握認為“寫作水平與喜好閱讀無關”
D.有97.5%的把握認為“寫作水平與喜好閱讀無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的部分圖象如圖所示:
的部分圖象如圖所示:
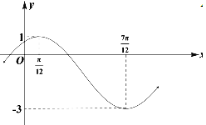
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的單調區間和對稱中心坐標;
的單調區間和對稱中心坐標;
(3)將![]() 的圖象向左平移
的圖象向左平移![]() 個單位,再將橫坐標伸長到原來的2倍,縱坐標不變,最后將圖象向上平移1個單位,得到函數
個單位,再將橫坐標伸長到原來的2倍,縱坐標不變,最后將圖象向上平移1個單位,得到函數![]() 的圖象,求函數
的圖象,求函數![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 下列結論錯誤的是
A. 命題:“若![]() ,則
,則![]() ”的逆否命題是“若
”的逆否命題是“若![]() ,則
,則![]() ”
”
B. “![]() ”是“
”是“![]() ”的充分不必要條件
”的充分不必要條件
C. 命題:“![]() ,
, ![]() ”的否定是“
”的否定是“![]() ,
, ![]() ”
”
D. 若“![]() ”為假命題,則
”為假命題,則![]() 均為假命題
均為假命題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com