
【題目】已知等差數列![]() 滿足
滿足![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,且滿足
,且滿足![]() .
.
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)數列![]() 滿足
滿足![]() ,求數列
,求數列![]() 的前
的前![]() 項和
項和![]() .
.
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和Sn滿足Sn=a(Sn﹣an+1)(a為常數,且a>0),且a3是6a1與a2的等差中項.
(1)求{an}的通項公式;
(2)設bn=anlog2an , 求數列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在Rt△AOB中,∠OAB= ![]() ,斜邊AB=4.Rt△AOC可以通過Rt△AOB以直線AO為軸旋轉得到,且二面角B﹣AO﹣C是直二面角,動點D在斜邊AB上.
,斜邊AB=4.Rt△AOC可以通過Rt△AOB以直線AO為軸旋轉得到,且二面角B﹣AO﹣C是直二面角,動點D在斜邊AB上.
(Ⅰ)求證:平面COD⊥平面AOB;
(Ⅱ)當VA﹣DOC:VA﹣BOC=1:2時,求CD與平面AOB所成角的大小.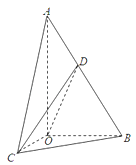
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,
中, ![]() 是拋物線
是拋物線![]() 的焦點,
的焦點, ![]() 是拋物線
是拋物線![]() 上的任意一點,當
上的任意一點,當![]() 位于第一象限內時,
位于第一象限內時, ![]() 外接圓的圓心到拋物線
外接圓的圓心到拋物線![]() 準線的距離為
準線的距離為![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)過![]() 的直線
的直線![]() 交拋物線
交拋物線![]() 于
于![]() 兩點,且
兩點,且![]() ,點
,點![]() 為
為![]() 軸上一點,且
軸上一點,且![]() ,求點
,求點![]() 的橫坐標
的橫坐標![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數y=f(x)的定義域為R,并且滿足f(x+y)=f(x)+f(y), ![]() ,且當x>0時,f(x)>0.
,且當x>0時,f(x)>0.
(1)求f(0)的值;
(2)判斷函數的奇偶性;
(3)如果f(x)+f(2+x)<2,求x取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,直線![]() 的參數方程為
的參數方程為![]() ,其中
,其中![]() 為參數,
為參數, ![]() ,再以坐標原點
,再以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,曲線
軸正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,其中
,其中![]() ,
, ![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)求![]() 的值;
的值;
(2)已知點![]() ,且
,且![]() ,求直線
,求直線![]() 的普通方程.
的普通方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com