
 已知函數
已知函數![]() 在點
在點![]() 處取得極大值
處取得極大值![]() ,其導函數
,其導函數![]() 的圖象經過點
的圖象經過點![]() ,
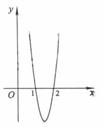
,![]() ,如圖所示.求:
,如圖所示.求:
(Ⅰ)![]() 的值;
的值;
(Ⅱ)![]() 的值.
的值.
解法一:
(Ⅰ)由圖象可知,在(-∝,1)上![]() (x)>0,在(1,2)上
(x)>0,在(1,2)上![]() (x)<0.
(x)<0.
在(2,+∝)上![]() (x)>0.
(x)>0.
故f(x)在(-∝,1),(2,+∝)上遞增,在(1,2)上遞減.
因此f(x)在x=1處取得極大值,所以x0=1.
(Ⅱ) ![]() (x)=3ax2+2bx+c,
(x)=3ax2+2bx+c,
由![]() (1)=0,
(1)=0, ![]() (2)=0, f(1)=5,
(2)=0, f(1)=5,
得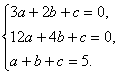 解得a=2,b=-9,c=12.
解得a=2,b=-9,c=12.
解法二:(Ⅰ)同解法一.
(Ⅱ)設![]() (x)=m(x-1)(x-2)=mx2-3mx+2m,
(x)=m(x-1)(x-2)=mx2-3mx+2m,
又![]() (x)=3ax2+2bx+c, 所以a=
(x)=3ax2+2bx+c, 所以a=![]() ,b=
,b=![]() ,c=2m
,c=2m
f(x)=![]() 由f(l)=5, 即
由f(l)=5, 即![]() 得m=6.
得m=6.
所以a=2,b=-9,c=12.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
(08年威海市質檢文) (14分)
已知函數![]() 在點
在點![]() 處取得極小值-4,使其導數
處取得極小值-4,使其導數![]() 的
的![]() 的取值范圍為
的取值范圍為![]() ,求:
,求:
(1)![]() 的解析式;
的解析式;
(2)若過點![]() 可作曲線
可作曲線![]() 的三條切線,求實數
的三條切線,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2015屆江蘇省高一下學期期末考試數學試卷(解析版) 題型:解答題
已知函數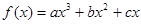 在點
在點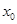 處取得極小值-4,使其導數
處取得極小值-4,使其導數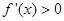 的
的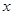 的取值范圍為
的取值范圍為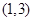 ,求:
,求:
(1)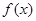 的解析式;
的解析式;
(2)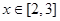 ,求
,求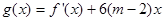 的最大值;
的最大值;
查看答案和解析>>
科目:高中數學 來源:2015屆江蘇省江都市高一下學期期末考試數學試卷(解析版) 題型:解答題
已知函數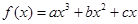 在點
在點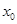 處取得極小值-4,使其導數
處取得極小值-4,使其導數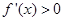 的
的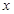 的取值范圍為
的取值范圍為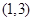 ,求:
,求:
(1)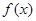 的解析式;
的解析式;
(2)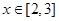 ,求
,求 的最大值;
的最大值;
查看答案和解析>>
科目:高中數學 來源:2013屆內蒙古高三第二次模擬考試理科數學試卷(解析版) 題型:解答題
(本題滿分12分)已知函數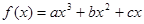 在點
在點 處取得極小值-4,使其導函數
處取得極小值-4,使其導函數 的
的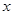 的取值范圍為(1,3)
的取值范圍為(1,3)
(Ⅰ)求 的解析式及
的解析式及 的極大值;
的極大值;
(Ⅱ)當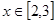 時,求
時,求 的最大值。
的最大值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com