
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)若![]() ,對任意
,對任意![]() ,不等式
,不等式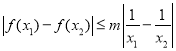 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)答案不唯一,見解析;(2) ![]()
【解析】
(1)先由題意得到定義域,對函數求導,分別討論![]() 和
和![]() 兩種情況,即可得出結果;
兩種情況,即可得出結果;
(2)因為![]() ,由(1)得到函數
,由(1)得到函數![]() 在
在![]() 上單調遞增,不妨設
上單調遞增,不妨設![]() ,則
,則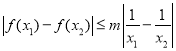 可化為
可化為![]() ,令
,令![]() ,則
,則![]() 為
為![]() 上的減函數,對
上的減函數,對![]() 求導,根據函數
求導,根據函數![]() 單調性,即可得出結果.
單調性,即可得出結果.
(1)∵依題意可知:函數![]() 的定義域為
的定義域為![]() ,
,
∴![]() ,
,
當![]() 時,
時,![]() 在
在![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上單調遞增.
上單調遞增.
當![]() 時,由
時,由![]() 得
得![]() ;由
;由![]() 得
得![]() ;
;
綜上可得當![]() 時,
時,![]() 在
在![]() 上單調遞增;
上單調遞增;
當![]() 時,
時,![]() 在
在![]() 上單調遞減;在
上單調遞減;在![]() 上單調遞增.
上單調遞增.
(2)因為![]() ,由(1)知,函數
,由(1)知,函數![]() 在
在![]() 上單調遞增,
上單調遞增,
不妨設![]() ,則
,則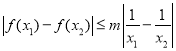 ,
,
可化為![]() ,
,
設![]() ,則
,則![]() ,
,
所以![]() 為
為![]() 上的減函數,
上的減函數,
即![]() 在
在![]() 上恒成立,等價于
上恒成立,等價于![]() 在
在![]() 上恒成立,
上恒成立,
設![]() ,所以
,所以![]() ,
,
因![]() ,所以
,所以![]() ,所以函數
,所以函數![]() 在
在![]() 上是增函數,
上是增函數,
所以![]() (當且僅當
(當且僅當![]() 時等號成立)
時等號成立)
所以![]() .
.


 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:高中數學 來源: 題型:
【題目】定義:若函數![]() 對任意的
對任意的![]() ,都有
,都有![]() 成立,則稱
成立,則稱![]() 為
為![]() 上的“淡泊”函數.
上的“淡泊”函數.
(1)判斷![]() 是否為
是否為![]() 上的“淡泊”函數,說明理由;
上的“淡泊”函數,說明理由;
(2)是否存在實數![]() ,使
,使![]() 為
為![]() 上的“淡泊”函數,若存在,求出
上的“淡泊”函數,若存在,求出![]() 的取值范圍;不存在,說明理由;
的取值范圍;不存在,說明理由;
(3)設![]() 是
是![]() 上的“淡泊”函數(其中
上的“淡泊”函數(其中![]() 不是常值函數),且
不是常值函數),且![]() ,若對任意的
,若對任意的![]() ,都有
,都有![]() 成立,求
成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種植基地將編號分別為1,2,3,4,5,6的六個不同品種的馬鈴薯種在如圖所示的
A | B | C | D | E | F |
這六塊實驗田上進行對比試驗,要求這六塊實驗田分別種植不同品種的馬鈴薯,若種植時要求編號1,3,5的三個品種的馬鈴薯中至少有兩個相鄰,且2號品種的馬鈴薯不能種植在A、F這兩塊實驗田上,則不同的種植方法有 ( )
A. 360種 B. 432種 C. 456種 D. 480種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
已知函數f(x)=![]() ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲線y=f(x)在點(2,f(2))處的切線方程;
(Ⅱ)若在區間![]() 上,f(x)>0恒成立,求a的取值范圍.
上,f(x)>0恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
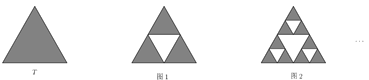
【題目】對于正三角形![]() ,挖去以三邊中點為頂點的小正三角形,得到一個新的圖形,這樣的過程稱為一次“鏤空操作“,設
,挖去以三邊中點為頂點的小正三角形,得到一個新的圖形,這樣的過程稱為一次“鏤空操作“,設![]() 是一個邊長為1的正三角形,第一次“鏤空操作”后得到圖1,對剩下的3個小正三角形各進行一次“鏤空操作”后得到圖2,對剩下的小三角形重復進行上述操作,設
是一個邊長為1的正三角形,第一次“鏤空操作”后得到圖1,對剩下的3個小正三角形各進行一次“鏤空操作”后得到圖2,對剩下的小三角形重復進行上述操作,設![]() 是第
是第![]() 次挖去的小三角形面積之和(如
次挖去的小三角形面積之和(如![]() 是第1次挖去的中間小三角形面積,
是第1次挖去的中間小三角形面積,![]() 是第2次挖去的三個小三角形面積之和),
是第2次挖去的三個小三角形面積之和),![]() 是前
是前![]() 次挖去的所有三角形的面積之和,則
次挖去的所有三角形的面積之和,則![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,點
,點![]() 、
、![]() 分別在線段
分別在線段![]() 、
、![]() 上,且
上,且![]() ,其中
,其中![]() ,連接
,連接![]() ,延長
,延長![]() 與
與![]() 的延長線交于點
的延長線交于點![]() ,連接
,連接![]() .
.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 時,求二面角
時,求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)若直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() 時,求
時,求![]() 值.
值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面直角坐標系xOy,在x軸的正半軸上,依次取點![]() ,
,![]() ,
,![]() ,
,![]() ,并在第一象限內的拋物線
,并在第一象限內的拋物線![]() 上依次取點
上依次取點![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,使得
,使得![]() 都為等邊三角形,其中
都為等邊三角形,其中![]() 為坐標原點,設第n個三角形的邊長為
為坐標原點,設第n個三角形的邊長為![]() .
.
⑴求![]() ,
,![]() ,并猜想
,并猜想![]() 不要求證明);
不要求證明);
⑵令![]() ,記
,記![]() 為數列
為數列![]() 中落在區間
中落在區間![]() 內的項的個數,設數列
內的項的個數,設數列![]() 的前m項和為
的前m項和為![]() ,試問是否存在實數
,試問是否存在實數![]() ,使得
,使得![]() 對任意
對任意![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范圍;若不存在,說明理由;
的取值范圍;若不存在,說明理由;
⑶已知數列![]() 滿足:
滿足:![]() ,數列
,數列![]() 滿足:
滿足:![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱![]() 中,
中,![]() ,
,![]() ,已知G與E分別為
,已知G與E分別為![]() 和
和![]() 的中點,D和F分別為線段AC和AB上的動點(不包括端點),若
的中點,D和F分別為線段AC和AB上的動點(不包括端點),若![]() ,則線段DF的長度的平方取值范圍為( ).
,則線段DF的長度的平方取值范圍為( ).

A.![]() B.
B.![]() C.
C. D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com