【題目】某企業生產A，B兩種產品，生產1噸A種產品需要煤4噸、電18千瓦；生產1噸B種產品需要煤1噸、電15千瓦。現因條件限制，該企業僅有煤10噸，并且供電局只能供電66千瓦，若生產1噸A種產品的利潤為10000元；生產1噸B種產品的利潤是5000元，試問該企業如何安排生產，才能獲得最大利潤？
科目：高中數學 來源： 題型：
【題目】已知函數f（x）滿足f（x+y）=f（x）+f（y），當x＞0時，有
，且f（1）=﹣2
（1）求f（0）及f（﹣1）的值；
（2）判斷函數f（x）的單調性，并利用定義加以證明；
（3）求解不等式f（2x）﹣f（x2+3x）＜4．
查看答案和解析>>
科目：高中數學 來源： 題型：
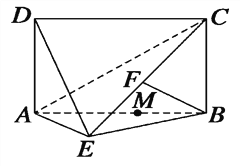
【題目】如圖，四邊形ABCD為矩形，DA⊥平面ABE，AE＝EB＝BC＝2，
BF⊥平面ACE，且點F在CE上．
(1)求證：AE⊥BE；
(2)求三棱錐D—AEC的體積；
(3)設點M在線段AB上，且滿足AM＝2MB，試在線段CE上確定一點N，
使得MN∥平面DAE.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司2016年前三個月的利潤(單位:百萬元)如下:
月份 |
|
|
|
利潤 |
|
|
|
（1）求利潤
關于月份
的線性回歸方程；
（2）試用(1)中求得的回歸方程預測
月和
月的利潤；
（3）試用(1)中求得的回歸方程預測該公司2016年從幾月份開始利潤超過
萬？
相關公式: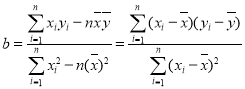 
, 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的焦距為
,左、右頂點分別為
、
,
是橢圓上一點, 記直線
、
的斜率為
、
,且有
.
（1）求橢圓
的方程；
（2）若直線
與橢圓交于
、
兩點, 以、為直徑的圓經過原點, 且線段
的垂直平分線在
軸上的截距為
,求直線
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
