
【題目】已知平面向量 ![]() =(1,x),
=(1,x), ![]() =(2x+3,﹣x)(x∈R).
=(2x+3,﹣x)(x∈R).
(1)若 ![]() ∥
∥ ![]() ,求|
,求| ![]() |
|
(2)若 ![]() 與
與 ![]() 夾角為銳角,求x的取值范圍.
夾角為銳角,求x的取值范圍.
(3)若| ![]() |=2,求與
|=2,求與 ![]() 垂直的單位向量
垂直的單位向量 ![]() 的坐標(biāo).
的坐標(biāo).
【答案】
(1)解:若 ![]() ,則﹣x﹣(2x+3)x=0,解得x=0或x=﹣2,
,則﹣x﹣(2x+3)x=0,解得x=0或x=﹣2,
當(dāng)x=0時(shí), ![]() =(﹣2,0),∴|
=(﹣2,0),∴| ![]() |=2,
|=2,
當(dāng)x=﹣2時(shí), ![]() =(2,﹣4),∴|
=(2,﹣4),∴| ![]() |=2
|=2 ![]()
(2)解:若 ![]() 與
與 ![]() 夾角為銳角,則
夾角為銳角,則 ![]() >0,即2x+3﹣x2>0,∴﹣1<x<3,
>0,即2x+3﹣x2>0,∴﹣1<x<3,
由(1)可知當(dāng)x=0時(shí), ![]() ,此時(shí)
,此時(shí) ![]() ,
, ![]() 的夾角為0,不符合題意,舍去,
的夾角為0,不符合題意,舍去,
∴x的取值范圍是(﹣1,0)∪(0,3)
(3)解:∵| ![]() |=2,∴1+x2=4,解得x=±
|=2,∴1+x2=4,解得x=± ![]() ,
,
設(shè) ![]() =(m,n),則m+nx=0,且m2+n2=1,
=(m,n),則m+nx=0,且m2+n2=1,
∴當(dāng)x= ![]() 時(shí),
時(shí), ![]() ,解得
,解得  或
或  ;
;
當(dāng)x=﹣ ![]() 時(shí),
時(shí), ![]() ,解得
,解得  或
或  ,
,
所以當(dāng)x= ![]() 時(shí),
時(shí), ![]() 的坐標(biāo)為(
的坐標(biāo)為( ![]() ,﹣
,﹣ ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() ),
),
當(dāng)x=﹣ ![]() 時(shí),
時(shí), ![]() 的坐標(biāo)為(
的坐標(biāo)為( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)根據(jù)向量平面列方程解出x,求出 ![]() 的坐標(biāo)即可得出|
的坐標(biāo)即可得出| ![]() |;(2)令cos<
|;(2)令cos< ![]() >>0,解出x,再去掉
>>0,解出x,再去掉 ![]() 共線的情況即可;(3)根據(jù)|
共線的情況即可;(3)根據(jù)| ![]() |=2計(jì)算x,設(shè)
|=2計(jì)算x,設(shè) ![]() =(m,n),列方程組解出即可.
=(m,n),列方程組解出即可.


 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]()
![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn)![]() ,一個(gè)焦點(diǎn)是
,一個(gè)焦點(diǎn)是![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若傾斜角為![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點(diǎn),且
兩點(diǎn),且![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓![]() (
(![]() )的離心率為
)的離心率為![]() ,
, ![]() 分別是它的左、右焦點(diǎn),且存在直線
分別是它的左、右焦點(diǎn),且存在直線![]() ,使
,使![]() 關(guān)于
關(guān)于![]() 的對(duì)稱點(diǎn)恰好是圓
的對(duì)稱點(diǎn)恰好是圓![]() (
(![]() )的一條直線的兩個(gè)端點(diǎn).
)的一條直線的兩個(gè)端點(diǎn).
(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)直線![]() 與拋物線
與拋物線![]() (
(![]() )相交于
)相交于![]() 兩點(diǎn),射線
兩點(diǎn),射線![]() ,
, ![]() 與橢圓
與橢圓![]() 分別相交于點(diǎn)
分別相交于點(diǎn)![]() ,試探究:是否存在數(shù)集
,試探究:是否存在數(shù)集![]() ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng)![]() 時(shí),總存在
時(shí),總存在![]() ,使點(diǎn)
,使點(diǎn)![]() 在以線段
在以線段![]() 為直徑的圓內(nèi)?若存在,求出數(shù)集
為直徑的圓內(nèi)?若存在,求出數(shù)集![]() ;若不存在,請(qǐng)說(shuō)明理由.
;若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知OPQ是半徑為1,圓心角為θ的扇形,A是扇形弧PQ上的動(dòng)點(diǎn),AB∥OQ,OP與AB交于點(diǎn)B,AC∥OP,OQ與AC交于點(diǎn)C.

(1)當(dāng)θ=![]() 時(shí),求點(diǎn)A的位置,使矩形ABOC的面積最大,并求出這個(gè)最大面積;
時(shí),求點(diǎn)A的位置,使矩形ABOC的面積最大,并求出這個(gè)最大面積;
(2)當(dāng)θ=![]() 時(shí),求點(diǎn)A的位置,使平行四邊形ABOC的面積最大,并求出這個(gè)最大面積.
時(shí),求點(diǎn)A的位置,使平行四邊形ABOC的面積最大,并求出這個(gè)最大面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某保險(xiǎn)公司有一款保險(xiǎn)產(chǎn)品的歷史收益率(收益率=利潤(rùn)÷保費(fèi)收入)的頻率分布直方圖如圖所示:

(Ⅰ)試估計(jì)平均收益率;
(Ⅱ)根據(jù)經(jīng)驗(yàn),若每份保單的保費(fèi)在20元的基礎(chǔ)上每增加![]() 元,對(duì)應(yīng)的銷量
元,對(duì)應(yīng)的銷量![]() (萬(wàn)份)與
(萬(wàn)份)與![]() (元)有較強(qiáng)線性相關(guān)關(guān)系,從歷史銷售記錄中抽樣得到如下5組
(元)有較強(qiáng)線性相關(guān)關(guān)系,從歷史銷售記錄中抽樣得到如下5組![]() 與
與![]() 的對(duì)應(yīng)數(shù)據(jù):
的對(duì)應(yīng)數(shù)據(jù):

據(jù)此計(jì)算出的回歸方程為![]() .
.
(i)求參數(shù)![]() 的估計(jì)值;
的估計(jì)值;
(ii)若把回歸方程![]() 當(dāng)作
當(dāng)作![]() 與
與![]() 的線性關(guān)系,用(Ⅰ)中求出的平均收益率估計(jì)此產(chǎn)品的收益率,每份保單的保費(fèi)定為多少元時(shí)此產(chǎn)品可獲得最大收益,并求出該最大收益.
的線性關(guān)系,用(Ⅰ)中求出的平均收益率估計(jì)此產(chǎn)品的收益率,每份保單的保費(fèi)定為多少元時(shí)此產(chǎn)品可獲得最大收益,并求出該最大收益.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知向量 ![]() =(sin
=(sin ![]() ,sin
,sin ![]() ),
), ![]() =(cos
=(cos ![]() ,cos
,cos ![]() ),且向量
),且向量 ![]() 與向量
與向量 ![]() 共線.
共線.
(1)求證:sin( ![]() ﹣
﹣ ![]() )=0;
)=0;
(2)若記函數(shù)f(x)=sin( ![]() ﹣
﹣ ![]() ),求函數(shù)f(x)的對(duì)稱軸方程;
),求函數(shù)f(x)的對(duì)稱軸方程;
(3)求f(1)+f(2)+f(3)+…+f(2013)的值;
(4)如果已知角0<A<B<π,且A+B+C=π,滿足f( ![]() )=f(
)=f( ![]() )=
)= ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】國(guó)際奧委會(huì)將于2017年9月15日在秘魯利馬召開(kāi)130次會(huì)議決定2024年第33屆奧運(yùn)會(huì)舉辦地。目前德國(guó)漢堡、美國(guó)波士頓等申辦城市因市民擔(dān)心賽事費(fèi)用超支而相繼退出。某機(jī)構(gòu)為調(diào)查我國(guó)公民對(duì)申辦奧運(yùn)會(huì)的態(tài)度,選了某小區(qū)的100位居民調(diào)查結(jié)果統(tǒng)計(jì)如下:

(1)根據(jù)已有數(shù)據(jù),把表格數(shù)據(jù)填寫(xiě)完整;
(2)能否在犯錯(cuò)誤的概率不超過(guò)5%的前提下認(rèn)為不同年齡與支持申辦奧運(yùn)無(wú)關(guān)?
(3)已知在被調(diào)查的年齡大于50歲的支持者中有5名女性,其中2位是女教師,現(xiàn)從這5名女性中隨機(jī)抽取3人,求至多有1位教師的概率.
附:  ,
, ![]() .
.
![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】現(xiàn)階段全國(guó)多地空氣質(zhì)量指數(shù)“爆表”.為探究車流量與![]() 濃度是否相關(guān),現(xiàn)對(duì)北方某中心城市的車流量最大的地區(qū)進(jìn)行檢測(cè),現(xiàn)采集到
濃度是否相關(guān),現(xiàn)對(duì)北方某中心城市的車流量最大的地區(qū)進(jìn)行檢測(cè),現(xiàn)采集到![]() 月某天
月某天![]() 個(gè)不同時(shí)段車流量與
個(gè)不同時(shí)段車流量與![]() 濃度的數(shù)據(jù),如下表:
濃度的數(shù)據(jù),如下表:
車流量 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根據(jù)上表中的數(shù)據(jù),用最小二乘法求出![]() 關(guān)于
關(guān)于![]() 的線性回歸方程;
的線性回歸方程;
(2)規(guī)定當(dāng)![]() 濃度平均值在
濃度平均值在![]() ,空氣質(zhì)量等級(jí)為優(yōu);當(dāng)
,空氣質(zhì)量等級(jí)為優(yōu);當(dāng)![]() 濃度平均值在
濃度平均值在![]() ,空氣質(zhì)量等級(jí)為良;為使該城市空氣質(zhì)量為優(yōu)和良,利用該回歸方程,預(yù)測(cè)要將車流量控制在每小時(shí)多少萬(wàn)輛內(nèi)(結(jié)果以萬(wàn)輛做單位,保留整數(shù)).
,空氣質(zhì)量等級(jí)為良;為使該城市空氣質(zhì)量為優(yōu)和良,利用該回歸方程,預(yù)測(cè)要將車流量控制在每小時(shí)多少萬(wàn)輛內(nèi)(結(jié)果以萬(wàn)輛做單位,保留整數(shù)).
附:回歸直線方程: ![]() ,其中
,其中 ,
, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在四棱錐![]() 中,
中, ![]() ,
,![]() ,
,![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() 是棱
是棱![]() 上的點(diǎn),
上的點(diǎn),![]() ,
,![]() ,
,![]() ,
,![]() .
.
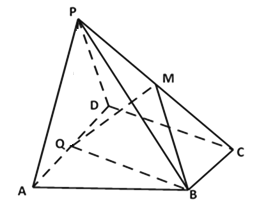
(1)求證:平面![]() 底面
底面![]() ;
;
(2)設(shè)![]() ,若二面角
,若二面角![]() 的平面角的大小為
的平面角的大小為![]() ,試確定
,試確定![]() 的值.
的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com