
【題目】在平面直角坐標(biāo)系![]() 中,橢圓
中,橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,直線
,直線![]() 被橢圓
被橢圓![]() 截得的線段長為
截得的線段長為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過原點的直線與橢圓![]() 交于
交于![]() ,
, ![]() 兩點(
兩點(![]() ,
, ![]() 不是橢圓
不是橢圓![]() 的頂點),點
的頂點),點![]() 在橢圓
在橢圓![]() 上,且
上,且![]() .直線
.直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() 兩點.設(shè)直線
兩點.設(shè)直線![]() 的斜率分別為
的斜率分別為![]() ,證明存在常數(shù)
,證明存在常數(shù)![]() 使得
使得![]() ,并求出
,并求出![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:
(Ⅰ)由離心率![]() 可得
可得![]() ,由對稱性直線
,由對稱性直線![]() 被橢圓截得弦長為
被橢圓截得弦長為![]() 可求得
可求得![]() 點坐標(biāo)為
點坐標(biāo)為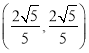 ,代入橢圓方程可求得
,代入橢圓方程可求得![]() 得橢圓標(biāo)準(zhǔn)方程;
得橢圓標(biāo)準(zhǔn)方程;
(Ⅱ)直線與橢圓相交,設(shè)![]() ,
, ![]() ,有
,有![]() ,由直線垂直得直線
,由直線垂直得直線![]() 的斜率為
的斜率為![]() .為了簡便設(shè)直線
.為了簡便設(shè)直線![]() 的方程為
的方程為![]() ,代入橢圓方程消元得
,代入橢圓方程消元得![]() 的一元二次方程.可得
的一元二次方程.可得![]() ,于是有
,于是有![]() ,而
,而![]() ,于是寫出直線
,于是寫出直線![]() 方程,求出
方程,求出![]() 點坐標(biāo),可得
點坐標(biāo),可得![]() ,比較可得
,比較可得![]() .
.
試題解析:
(Ⅰ)∵![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() .①
.①
設(shè)直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,不妨設(shè)點
兩點,不妨設(shè)點![]() 為第一象限內(nèi)的交點.∴
為第一象限內(nèi)的交點.∴![]() ,
,
∴![]() 代入橢圓方程可得
代入橢圓方程可得![]() .②
.②
由①②知![]() ,
,![]() ,所以橢圓的方程為:
,所以橢圓的方程為:![]() .
.
(Ⅱ)設(shè)![]()
![]() ,則
,則![]() ,
,
直線![]() 的斜率為
的斜率為![]() ,又
,又![]() ,
,
故直線![]() 的斜率為
的斜率為![]() .設(shè)直線
.設(shè)直線![]() 的方程為
的方程為![]() ,
,
由題知![]() ,
,![]() 聯(lián)立
聯(lián)立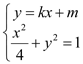 ,得
,得![]()
![]() .
.
∴![]() ,
,![]()
![]() ,由題意知
,由題意知![]() ,
,
∴![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
令![]() ,得
,得![]() ,即
,即![]() ,可得
,可得![]()
![]() ,∴
,∴![]() ,即
,即![]() .
.
因此存在常數(shù)![]() 使得結(jié)論成立.
使得結(jié)論成立.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖⑴、⑵、⑶、⑷為四個幾何體的三視圖,根據(jù)三視圖可以判斷這四個幾何體依次分別為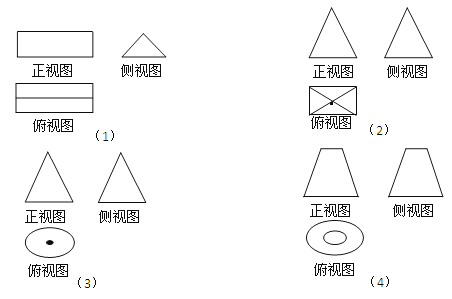
A.三棱臺、三棱柱、圓錐、圓臺
B.三棱臺、三棱錐、圓錐、圓臺
C.三棱柱、正四棱錐、圓錐、圓臺
D.三棱柱、三棱臺、圓錐、圓臺
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙兩位學(xué)生參加數(shù)學(xué)競賽培訓(xùn),現(xiàn)分別從他們在培訓(xùn)期間參加的若干次預(yù)賽成績中隨機抽取8次,記錄如下:
甲 | 82 | 81 | 79 | 78 | 95 | 88 | 93 | 84 |
乙 | 92 | 95 | 80 | 75 | 83 | 80 | 90 | 85 |
(1)用莖葉圖表示這兩組數(shù)據(jù);
(2)現(xiàn)要從中選派一人參加數(shù)學(xué)競賽,從統(tǒng)計學(xué)的角度(在平均數(shù)、方差或標(biāo)準(zhǔn)差中選兩個)考慮,你認(rèn)為選派哪位學(xué)生參加合適?請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知f(x)是定義在R上的奇函數(shù),當(dāng)x≥0時,f(x)=x2﹣3x,則函數(shù)g(x)=f(x)﹣x+3的零點的集合為( )
A.{1,3}
B.{﹣3,﹣1,1,3}
C.{2﹣ ![]() ,1,3}
,1,3}
D.{﹣2﹣ ![]() ,1,3}
,1,3}
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)等差數(shù)列{an}滿足a3=5,a10=﹣9.
(1)求{an}的通項公式;
(2)求{an}的前n項和Sn及使得Sn最大的序號n的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè){an}是一個公差不為零的等差數(shù)列,其前n項和為Sn , 已知S9=90,且a1 , a2 , a4成等比數(shù)列.
(1)求數(shù)列{an}的通項公式;
(2)設(shè)bn= ![]() ,求數(shù)列{bn}的前n項和Tn .
,求數(shù)列{bn}的前n項和Tn .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=sin(ωx+φ)其中ω>0,|φ|< ![]() .
.
(1)若cos ![]() cosφ﹣sin
cosφ﹣sin ![]() sinφ=0.求φ的值;
sinφ=0.求φ的值;
(2)在(1)的條件下,若函數(shù)f(x)的圖象的相鄰兩條對稱軸之間的距離等于 ![]() ,求函數(shù)f(x)的解析式;并求最小正實數(shù)m,使得函數(shù)f(x)的圖象象左平移m個單位所對應(yīng)的函數(shù)是偶函數(shù).
,求函數(shù)f(x)的解析式;并求最小正實數(shù)m,使得函數(shù)f(x)的圖象象左平移m個單位所對應(yīng)的函數(shù)是偶函數(shù).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com