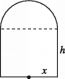
【題目】某制瓶廠要制造一批軸截面如圖所示的瓶子,瓶子是按照統(tǒng)一規(guī)格設(shè)計的,瓶體上部為半球體,下部為圓柱體,并保持圓柱體的容積為3π.設(shè)圓柱體的底面半徑為x,圓柱體的高為h,瓶體的表面積為S.
(1)寫出S關(guān)于x的函數(shù)關(guān)系式;
(2)如何設(shè)計瓶子的尺寸(不考慮瓶壁的厚度),可以使表面積S最小,并求出最小值.
【答案】（1）S=3πx2+
(x>0).（2）當圓柱體的底面半徑為1時,可使表面積S取得最小值9π.
【解析】
（1）根據(jù)體積公式求出h，再根據(jù)表面積公式計算即可得到S與x的關(guān)系式，
（2）根據(jù)導數(shù)和函數(shù)的最值得關(guān)系即可求出．
解:(1)據(jù)題意可知πx2h=3π,得h=
,
則S=·4πx2+πx2+2πx·=3πx2+
(x>0).
(2)S'=6πx-
,
令S'=0,得x=1.列表如下:
x | (0,1) | 1 | (1,+∞) |
S' | - | 0 | + |
S | ↘ | 極小值9π | ↗ |
當x=1時,S取得極小值,且是最小值,
故當圓柱體的底面半徑為1時,可使表面積S取得最小值9π.
科目：高中數(shù)學 來源： 題型：
【題目】數(shù)列{an}滿足a1= 
，an+1=an2﹣an+1（n∈N*），則m= 
+ 
+…+ 
的整數(shù)部分是（ ）
A.0
B.1
C.2
D.3
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設(shè)集合A={1，2，6}，B={2，4}，C={1，2，3，4}，則（A∪B）∩C=（ ）
A.{2}
B.{1，2，4}
C.{1，2，4，6}
D.{1，2，3，4，6}
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】下列函數(shù)中，在其定義域內(nèi)既是奇函數(shù)又是單調(diào)遞增的函數(shù)是（ ）
A.y=﹣ 
B.y=3﹣x﹣3x
C.y=x|x|
D.y=x3﹣x
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橫梁的強度和它的矩形橫斷面的長的平方與寬的乘積成正比,要將直徑為d的圓木鋸成強度最大的橫梁,則橫斷面的長和寬分別為 ( )
A. 
d, 
d B. d, 
d
C. d, d D. d, d
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設(shè)向量 
=（ 
sinx，sinx）， 
=（cosx，sinx），x∈（0， 
）．
（1）若| |=| |，求x的值；
（2）設(shè)函數(shù)f（x）= 
，求f（x）的最大值．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某個體戶計劃經(jīng)銷A，B兩種商品，據(jù)調(diào)查統(tǒng)計，當投資額為x(x≥0)萬元時，在經(jīng)銷A，B商品中所獲得的收益分別為f(x)萬元與g(x)萬元，其中f(x)＝a(x－1)＋2，g(x)＝6ln(x＋b)(a＞0，b＞0)．已知投資額為零時收益為零．
(1)求a，b的值；
(2)如果該個體戶準備投入5萬元經(jīng)銷這兩種商品，請你幫他制定一個資金投入方案，使他能獲得最大利潤．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在△ABC中，角A，B，C的對邊分別是a，b，c，已知(a－3b)cos C＝c(3cos B－cos A)．
(1)求
的值； (2)若c＝
a，求角C的大小．
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】在平面直角坐標系xOy中，曲線C1的參數(shù)方程為
(α為參數(shù))，以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，直線l的極坐標方程為
，曲線C2的極坐標方程為
(a>0)．
(1)求直線l與曲線C1的交點的極坐標(ρ，θ)(ρ≥0，0≤θ<2π)；
(2)若直線l與C2相切，求a的值．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com