【題目】設
、
是兩條不同的直線，
、
、
是三個不同的平面，則
的一個充分條件是（ ）
A.存在一條直線，
，
B.存在一條直線，
，
C.存在一個平面，滿足
，
D.存在兩條異面直線，，，
，，
【答案】CD
【解析】
A、B選項，直接判斷出
、
的位置關系；C選項，利用面面平行的性質可判斷、的位置關系；D選項，根據面面平行的判定定理可判斷、的位置關系.結合充分條件的定義可得出結論.
對于選項A，若存在一條直線
，
，
，則
或與相交.
若，則存在一條直線，使得
，，
所以選項A的內容是的一個必要條件而不是充分條件；
對于選項B，存在一條直線，
，，則或與相交.
若，則存在一條直線，，，
所以，選項B的內容是的一個必要條件而不是充分條件；
對于選項C，平行于同一個平面的兩個平面顯然是平行的，故選項C的內容是的一個充分條件；
對于選項D，可以通過平移把兩條異面直線平移到其中一個平面
中，成為相交直線，由面面平行的判定定理可知
，
，則，
所以選項D的內容是的一個充分條件.
故選：CD.
應用題作業本系列答案科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P－ABCD中，已知PA⊥平面ABCD，且四邊形ABCD為直角梯形，∠ABC＝∠BAD＝
，PA＝AD＝2，AB＝BC＝1，點M、E分別是PA、PD的中點
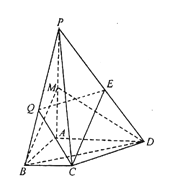
(1)求證：CE//平面BMD
(2)點Q為線段BP中點，求直線PA與平面CEQ所成角的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某工廠共有男女員工500人，現從中抽取100位員工對他們每月完成合格產品的件數統計如下：
每月完成合格產品的件數（單位：百件） |
|
|
|
|
|
頻數 | 10 | 45 | 35 | 6 | 4 |
男員工人數 | 7 | 23 | 18 | 1 | 1 |
（1）其中每月完成合格產品的件數不少于3200件的員工被評為“生產能手”.由以上統計數據填寫下面
列聯表，并判斷是否有95%的把握認為“生產能手”與性別有關？
非“生產能手” | “生產能手” | 合計 | |
男員工 | |||
span>女員工 | |||
合計 |
（2）為提高員工勞動的積極性，工廠實行累進計件工資制：規定每月完成合格產品的件數在定額2600件以內的，計件單價為1元；超出
件的部分，累進計件單價為1.2元；超出
件的部分，累進計件單價為1.3元；超出400件以上的部分，累進計件單價為1.4元.將這4段中各段的頻率視為相應的概率，在該廠男員工中選取1人，女員工中隨機選取2人進行工資調查，設實得計件工資（實得計件工資=定額計件工資+超定額計件工資）不少于3100元的人數為，求的分布列和數學期望.
附：
，
.
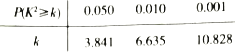查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列四個命題：
①函數
與函數
表示同一個函數；
②奇函數的圖象一定通過直角坐標系的原點；
③函數
的圖象可由
的圖象向右平移1個單位得到；
④若函數
的定義域為
，則函數
的定義域為
；
⑤設函數是在區間
上圖象連續的函數，且
，則方程
在區間上至少有一實根．
其中正確命題的序號是________．（填上所有正確命題的序號）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若函數f（x）=e2x﹣ax2+1在[1，2]上是減函數，則實數a的取值范圍是（ ）
A. [
，+∞） B. （，+∞） C. [
，+∞） D. （，+∞）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】《中華人民共和國民法總則》（以下簡稱《民法總則》）自2017年10月1日起施行.作為民法典的開篇之作，《民法總則》與每個人的一生息息相關.某地區為了調研本地區人們對該法律的了解情況，隨機抽取50人，他們的年齡都在區間
上，年齡的頻率分布及了解《民法總則》的入數如下表：
年齡 |
|
|
|
|
|
|
頻數 | 5 | 5 | 10 | 15 | 5 | 10 |
了解《民法總則》 | 1 | 2 | 8 | 12 | 4 | 5 |
（1）填寫下面
列聯表，并判斷是否有
的把握認為以45歲為分界點對了解《民法總則》政策有差異；
年齡低于45歲的人數 | 年齡不低于45歲的人數 | 合計 | |
了解 |
|
| |
不了解 |
|
| |
合計 |
（2）若對年齡在
，
的被調研人中各隨機選取2人進行深入調研，記選中的4人中不了解《民法總則》的人數為
，求隨機變量的分布列和數學期望.
參考公式和數據：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】《五曹算經》是我國南北朝時期數學家甄鸞為各級政府的行政人員編撰的一部實用算術書.其第四卷第九題如下：“今有平地聚粟，下周三丈高四尺，問粟幾何？”其意思為“場院內有圓錐形稻谷堆，底面周長3丈，高4尺，那么這堆稻谷有多少斛？”已知1丈等于10尺，1斜稻谷的體積約為1.62立方尺，圓周率約為3，估算出堆放的稻谷約有（ ）
A.57.08斜B.171.24斛C.61.73斛D.185.19斛
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
