
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;
處的切線方程;
(2)對于任意的![]() ,
,![]() 的圖象恒在
的圖象恒在![]() 圖象的上方,求實(shí)數(shù)a的取值菹圍.
圖象的上方,求實(shí)數(shù)a的取值菹圍.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)求出![]() 的值可得切點(diǎn)坐標(biāo),求出
的值可得切點(diǎn)坐標(biāo),求出![]() 的值,可得切線斜率,利用點(diǎn)斜式可得曲線
的值,可得切線斜率,利用點(diǎn)斜式可得曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程;(2)由題意得
處的切線方程;(2)由題意得![]() 在
在![]() 恒成立,令
恒成立,令![]() ,則需求出函數(shù)
,則需求出函數(shù)![]() 的最小值即可,但由于
的最小值即可,但由于![]() 的零點(diǎn)不易求出,故通過再次求導(dǎo)的方法逐步求解,進(jìn)而求得
的零點(diǎn)不易求出,故通過再次求導(dǎo)的方法逐步求解,進(jìn)而求得![]() 的最小值.
的最小值.
(1)當(dāng)![]() 時,
時,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴函數(shù)![]() 在點(diǎn)
在點(diǎn)![]() 處的切線方程為
處的切線方程為![]() ,
,
即![]() .
.
(2)由題知當(dāng)![]() 時,
時,![]() 恒成立,
恒成立,
即當(dāng)![]() 時,
時,![]() 恒成立,
恒成立,
等價于![]() 在
在![]() 恒成立.
恒成立.
令![]() ,
,
則![]() ,
,
令![]() ,則
,則![]() ,
,
∴![]() 在
在![]() 上單調(diào)遞增,且
上單調(diào)遞增,且![]() ,
,![]()
![]() 存在唯一零點(diǎn)
存在唯一零點(diǎn)![]() ,
,
使得![]() ,
,
且當(dāng)![]() 時,
時,![]() ,
,![]() 單調(diào)遞減;當(dāng)
單調(diào)遞減;當(dāng)![]() 時,
時,![]() ,
,![]() 單調(diào)遞增.
單調(diào)遞增.
∴![]() .
.
由![]() ,得
,得![]() ,
,
∴![]() ,
,
即![]() .
.
設(shè)![]() ,則
,則![]() ,
,
∴![]() 在
在![]() 單調(diào)遞增.
單調(diào)遞增.
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
故實(shí)數(shù)![]() 的取值范圍為
的取值范圍為![]() .
.


 小學(xué)課時特訓(xùn)系列答案
小學(xué)課時特訓(xùn)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在矩形ABCD和矩形ABEF中,![]() ,
,![]() ,矩形ABEF可沿AB任意翻折.
,矩形ABEF可沿AB任意翻折.

(1)求證:當(dāng)點(diǎn)F,A,D不共線時,線段MN總平行于平面ADF.
(2)“不管怎樣翻折矩形ABEF,線段MN總與線段FD平行”這個結(jié)論正確嗎?如果正確,請證明;如果不正確,請說明能否改變個別已知條件使上述結(jié)論成立,并給出理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
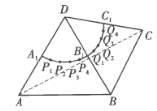
【題目】如圖,正四面體![]() 的各棱長均為2,
的各棱長均為2,![]() 、
、![]() 、
、![]() 分別為棱
分別為棱![]() 、
、![]() 、
、![]() 的中點(diǎn),以
的中點(diǎn),以![]() 為圓心、1為半徑,分別在面
為圓心、1為半徑,分別在面![]() 、面
、面![]() 內(nèi)作弧
內(nèi)作弧![]() ,并將兩弧各分成五等份,分點(diǎn)順次為
,并將兩弧各分成五等份,分點(diǎn)順次為![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 以及
以及![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .一只甲蟲欲從點(diǎn)
.一只甲蟲欲從點(diǎn)![]() 出發(fā),沿四面體表面爬行至點(diǎn)
出發(fā),沿四面體表面爬行至點(diǎn)![]() ,則其爬行的最短距離為___________。
,則其爬行的最短距離為___________。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公園內(nèi)有一塊以![]() 為圓心半徑為
為圓心半徑為![]() 米的圓形區(qū)域.為豐富市民的業(yè)余文化生活,現(xiàn)提出如下設(shè)計方案:如圖,在圓形區(qū)域內(nèi)搭建露天舞臺,舞臺為扇形
米的圓形區(qū)域.為豐富市民的業(yè)余文化生活,現(xiàn)提出如下設(shè)計方案:如圖,在圓形區(qū)域內(nèi)搭建露天舞臺,舞臺為扇形![]() 區(qū)域,其中兩個端點(diǎn)
區(qū)域,其中兩個端點(diǎn)![]() ,
,![]() 分別在圓周上;觀眾席為梯形
分別在圓周上;觀眾席為梯形![]() 內(nèi)切在圓
內(nèi)切在圓![]() 外的區(qū)域,其中
外的區(qū)域,其中![]() ,
,![]() ,且
,且![]() ,
,![]() 在點(diǎn)
在點(diǎn)![]() 的同側(cè).為保證視聽效果,要求觀眾席內(nèi)每一個觀眾到舞臺
的同側(cè).為保證視聽效果,要求觀眾席內(nèi)每一個觀眾到舞臺![]() 處的距離都不超過
處的距離都不超過![]() 米.設(shè)
米.設(shè)![]() ,
,![]() .問:對于任意
.問:對于任意![]() ,上述設(shè)計方案是否均能符合要求?
,上述設(shè)計方案是否均能符合要求?

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,討論函數(shù)
時,討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(2)若函數(shù)![]() 有兩個極值點(diǎn)
有兩個極值點(diǎn)![]() ,
,![]() ,證明:
,證明: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給圖中A,B,C,D,E,F六個區(qū)域進(jìn)行染色,每個區(qū)域只染一種顏色,且相鄰的區(qū)域不同色.若有4種顏色可供選擇,則共有___種不同的染色方案.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 的方程為
的方程為![]() .
.
(1)求過點(diǎn)![]() 且與圓
且與圓![]() 相切的直線
相切的直線![]() 的方程;
的方程;
(2)直線![]() 過點(diǎn)
過點(diǎn)![]() ,且與圓
,且與圓![]() 交于
交于![]() 、
、![]() 兩點(diǎn),若
兩點(diǎn),若![]() ,求直線
,求直線![]() 的方程;
的方程;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知點(diǎn)![]() ,圓
,圓![]() .
.
(1)若直線![]() 過點(diǎn)
過點(diǎn)![]() 且到圓心
且到圓心![]() 的距離為
的距離為![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)設(shè)過點(diǎn)![]() 的直線
的直線![]() 與圓
與圓![]() 交于
交于![]() 、
、![]() 兩點(diǎn)(
兩點(diǎn)(![]() 的斜率為負(fù)),當(dāng)
的斜率為負(fù)),當(dāng)![]() 時,求以線段
時,求以線段![]() 為直徑的圓的方程.
為直徑的圓的方程.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com