
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以直角坐標系的原點
為參數).以直角坐標系的原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立坐標系,曲線
軸的正半軸為極軸建立坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)若過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,與
兩點,與![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸,建立極坐標系,直線
軸正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線![]() 的普通方程與直線
的普通方程與直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
, ![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某餐廳通過查閱了最近5次食品交易會參會人數![]() (萬人)與餐廳所用原材料數量
(萬人)與餐廳所用原材料數量![]() (袋),得到如下統計表:
(袋),得到如下統計表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
參會人數 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根據所給5組數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() .
.
(2)已知購買原材料的費用![]() (元)與數量
(元)與數量![]() (袋)的關系為
(袋)的關系為![]() ,
,
投入使用的每袋原材料相應的銷售收入為700元,多余的原材料只能無償返還,據悉本次交易大會大約有15萬人參加,根據(1)中求出的線性回歸方程,預測餐廳應購買多少袋原材料,才能獲得最大利潤,最大利潤是多少?(注:利潤![]() 銷售收入
銷售收入![]() 原材料費用).
原材料費用).
參考公式:  ,
, ![]() .
.
參考數據: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某村計劃建造一個室內面積為800m2的矩形蔬菜溫室,在室內,沿左、右兩側與后側內墻各保留1m寬的通道,沿前側內墻保留3m寬的空地.當矩形溫室的邊長各為多少時,蔬菜的種植面積最大?最大種植面積是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() 的定義域為
的定義域為![]() ,若滿足條件:存在
,若滿足條件:存在![]() ,使
,使![]() 在
在![]() 上的值域為
上的值域為![]() ,則稱
,則稱![]() 為“倍縮函數”.若函數
為“倍縮函數”.若函數![]() 為“倍縮函數”,則實數
為“倍縮函數”,則實數![]() 的取值范圍是
的取值范圍是
A. (﹣∞,ln2﹣1) B. (﹣∞,ln2﹣1]
C. (1﹣ln2,+∞) D. [1﹣ln2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,點
中,點![]() 的坐標為
的坐標為![]() ,直線
,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,以
為極點,以![]() 軸的非負半軸為極軸,選擇相同的單位長度建立極坐標系,圓
軸的非負半軸為極軸,選擇相同的單位長度建立極坐標系,圓![]() 極坐標方程為
極坐標方程為![]() .
.
(Ⅰ)當![]() 時,求直線
時,求直線![]() 的普通方程和圓
的普通方程和圓![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)直線![]() 與圓
與圓![]() 的交點為
的交點為![]() 、
、![]() ,證明:
,證明:![]() 是與
是與![]() 無關的定值.
無關的定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某市3月1日至14日的空氣質量指數趨勢圖.空氣質量指數小于100表示空氣質量優良,空氣質量指數大于200表示空氣重度污染.某人隨機選擇3月1日至3月13日中的某一天到達該市,并停留2天.
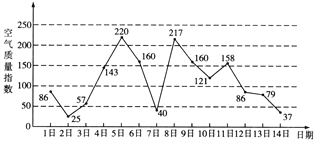
(Ⅰ)求3月1日到14日空氣質量指數的中位數;
(Ⅱ)求此人到達當日空氣重度污染的概率;
(Ⅲ)由圖判斷從哪天開始連續三天的空氣質量指數方差最大?(結論不要求證明)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com