在△
ABC中,
a=3,
b=2
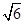
,∠
B=2∠
A.
(1)求cos
A的值;
(2)求
c的值.
(1)

(2)5
(1)在△
ABC中,由正弦定理

∴cos
A=

.
(2)由余弦定理,
a2=
b2+
c2-2
bccos
A⇒3
2=(2
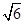
)
2+
c2-2×2
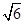 c
c×

,
則
c2-8
c+15=0.∴
c=5或
c=3.
當
c=3時,
a=
c,∴
A=
C.
由
A+
B+
C=π,知
B=

,與
a2+
c2≠
b2矛盾.
∴
c=3舍去.故
c的值為5.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
在△
ABC中,已知
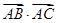
=3
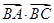
.
(1)求證:tan
B=3tan
A;
(2)若cos
C=
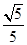
,求
A的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在銳角
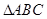
中,角
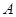
,
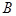
,
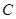
對應的邊分別是
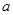
,
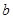
,
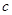
.已知
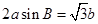
.
(1)求角
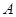
的大小;
(2)若
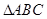
的面積
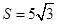
,
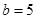
,求
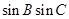
的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知函數(shù)
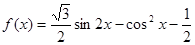
,
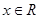
(I)若
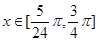
,求函數(shù)
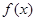
的最大值和最小值,并寫出相應的x的值;
(II)設
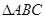
的內角
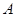
、
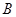
、
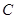
的對邊分別為
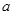
、
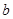
、
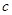
,滿足
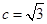
,
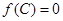
且
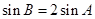
,求
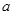
、
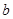
的值
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在△ABC中,角A、B、C的對邊分別為a、b、c,若b-
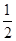
c=acosC,則A等于( )
(A)
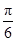
(B)
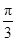
(C)
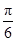
或
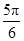
(D)
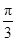
或
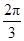
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
在△
ABC中,角
A,
B,
C的對邊分別為
a,
b,
c,且2cos
2
cos
B-sin(
A-
B)sin
B+cos(
A+
C)=-

.
(1)求cos
A的值;
(2)若
a=4

,
b=5,求向量

在
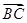
方向上的投影.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在△
ABC中,∠
ABC=

,
AB=
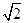
,
BC=3,則sin ∠
BAC=( ).
查看答案和解析>>

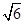 ,∠B=2∠A.
,∠B=2∠A.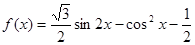 ,
,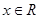
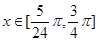 ,求函數(shù)
,求函數(shù)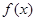 的最大值和最小值,并寫出相應的x的值;
的最大值和最小值,并寫出相應的x的值; 的內角
的內角 、
、 、
、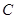 的對邊分別為
的對邊分別為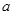 、
、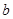 、
、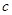 ,滿足
,滿足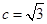 ,
,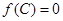 且
且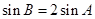 ,求
,求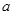 、
、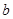 的值
的值  cos B-sin(A-B)sin B+cos(A+C)=-
cos B-sin(A-B)sin B+cos(A+C)=- .
. ,b=5,求向量
,b=5,求向量 在
在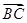 方向上的投影.
方向上的投影.