
���}Ŀ����������![]() ��߅�L��2�������ظ�
��߅�L��2�������ظ�![]() ���ۣ�ʹ�c(di��n)
���ۣ�ʹ�c(di��n)![]() �c�c(di��n)
�c�c(di��n)![]() �g�ľ��x��
�g�ľ��x��![]() ���˕r(sh��)�����w
���˕r(sh��)�����w![]() ��������e��__________��
��������e��__________��
���𰸡�![]()
�����������������}�⌢���w�a(b��)�Ξ����������Y(ji��)���������Ď���������Ӌ(j��)�㼴�������K�Y(ji��)��.
Ԕ�⣺����(j��)�}���֪�����FBACD�����l��(c��)��BD��AD��DC��DA��
�����ǵ��������Σ����������������U(ku��)չ���������������
����������ĵ��������B�������c(di��n)����c(di��n)�ľ��x��������İ돽��
�������ĵ���߅�L��1,1,![]() ��
��
���}��ɵã����������µ������c(di��n)�B�������c(di��n)������������c(di��n)�ľ��x��ȣ��f�����ľ������������ģ�
�������������������Ğ�O�������İ돽��r��
�����ĸߞ�![]() ,���ĵ�����ľ��x��
,���ĵ�����ľ��x��![]() ��
��
��������,�����BDC,BD=CD=1,BC=![]() ,���BDC=120�㣬
,���BDC=120�㣬
��BDC����ӈA�İ돽�飺![]() ��
��
����İ돽��![]() .
.
�����ı���e�飺![]() .
.
�ʴ𰸞飺![]() .
.


 ���б�ˢ�}ϵ�д�
���б�ˢ�}ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���^���タy2=4x�Ľ��c(di��n)F��ֱ�������タ��A��B���c(di��n)����|AF|=2|BF|���tֱ��AB��б�ʞ飨 ��
A.![]()
B.![]()
C.![]() ��
�� ![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���҇��Ŵ���(sh��)�W(xu��)�������������g(sh��)���������}���������ѣ�ˮ��ֲ��������һ�գ��L���ߣ�ݸ��ֲ�������Qˮ�[��ϯ�Ӳݣ���һ�գ��Lһ�ߣ��������룬ݸ�����Ա��������ն��L�ȣ�����˼�ǣ����������L1�գ��L��3�ߣ�ݸ���L1�գ��L��1�ߣ��ѵ����L���՜p�룬ݸ�����L��������1�������ѡ�ݸ�L����ȣ��t����ĕr(sh��)�g�s���գ����Y(ji��)������һλС��(sh��)��������(sh��)��(j��)��lg2��0.30��lg3��0.48��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�A ![]() ��
�� ![]() ������
������ ![]() ��A�ģ��ϵ�ÿһ�c(di��n)�M����(bi��o)��׃���v����(bi��o)׃?y��u)�ԭ����һ�룬�õ�����
��A�ģ��ϵ�ÿһ�c(di��n)�M����(bi��o)��׃���v����(bi��o)׃?y��u)�ԭ����һ�룬�õ����� ![]() .
.
��1�������� ![]() �ķ��̣�
�ķ��̣�
��2�����c(di��n) ![]() ������
������ ![]() ��һ�c(di��n)���^�c(di��n)
��һ�c(di��n)���^�c(di��n) ![]() ������
������ ![]() ������A
���о����A ![]() �ڲ�ͬ�ă��c(di��n)
�ڲ�ͬ�ă��c(di��n) ![]() ������
������ ![]() ��
�� ![]() ���҂�(c��)������֪�c(di��n)
���҂�(c��)������֪�c(di��n) ![]() .����߅��
.����߅�� ![]() ��e�����ֵ.
��e�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ij���S���a(ch��n)ij�N�a(ch��n)Ʒ��ÿ���a(ch��n)1���a(ch��n)Ʒ���˹��M(f��i)4�fԪ��ÿ��߀��̶��ɱ�3�fԪ.��(j��ng)�^�L���{(di��o)��y(t��ng)Ӌ(j��)��ÿ�յ��N���~![]() ����λ���fԪ���c�ծa(ch��n)��
����λ���fԪ���c�ծa(ch��n)��![]() ����λ�������M�㺯��(sh��)�P(gu��n)ϵ
����λ�������M�㺯��(sh��)�P(gu��n)ϵ ����֪ÿ�����a(ch��n)4���r(sh��)������7�fԪ.
����֪ÿ�����a(ch��n)4���r(sh��)������7�fԪ.
��1����![]() ��ֵ��
��ֵ��
��2����(d��ng)�ծa(ch��n)������ه��r(sh��)��ÿ���������������������٣�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��һ��(g��)�����w��ƽ��չ�_�D��ԓ�����w��ֱ�^�D��ʾ��D��D��ʾ.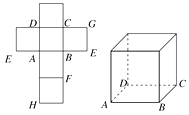
��1��Ո����ĸF��G��H��(bi��o)ӛ�������w����(y��ng)����c(di��n)̎(����Ҫ�f������)��
��2���Д�ƽ��BEG�cƽ��ACH��λ���P(gu��n)ϵ�����f����ĽY(ji��)Փ��
��3���C����ֱ��DF��ƽ��BEG.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪�E�A ![]() ���ҽ��c(di��n)��
���ҽ��c(di��n)�� ![]() ������c(di��n)��
������c(di��n)�� ![]() ��
�� ![]() ���L��
���L�� ![]() ���x���ʞ�
���x���ʞ� ![]() .
.
��1����E�A ![]() �ķ��̣�
�ķ��̣�
��2�����c(di��n) ![]() �ǙE�A
�ǙE�A ![]() �ϵ�һ���ރ�(n��i)��һ��(g��)�c(di��n)��ֱ��
�ϵ�һ���ރ�(n��i)��һ��(g��)�c(di��n)��ֱ�� ![]() �^�c(di��n)
�^�c(di��n) ![]() ���cֱ��
���cֱ�� ![]() ƽ�У�ֱ��
ƽ�У�ֱ�� ![]() ��
�� ![]() �c�E�A
�c�E�A ![]() ����
���� ![]() ���c(di��n)���c
���c(di��n)���c ![]() �����c(di��n)
�����c(di��n) ![]() ���Ƿ���ڳ���(sh��)
���Ƿ���ڳ���(sh��) ![]() ��ʹ
��ʹ ![]() .�����ڣ����
.�����ڣ���� ![]() ��ֵ���������ڣ�Ո�f������.
��ֵ���������ڣ�Ո�f������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��![]() �M��
�M��![]() ����
����![]() ����ǰn�(xi��ng)֮�͞�Sn���t�M�㲻��ʽ
����ǰn�(xi��ng)֮�͞�Sn���t�M�㲻��ʽ![]() ����С��Ȼ��(sh��)n�� ___.
����С��Ȼ��(sh��)n�� ___.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
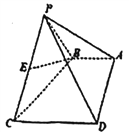
���}Ŀ����D�������F![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ���c(di��n).
���c(di��n).
��1���C����![]() ƽ��
ƽ��![]() ��
��
��2����![]() ƽ��
ƽ��![]() ��
��![]() ��߅�L��
��߅�L��![]() ���������Σ���ֱ��
���������Σ���ֱ��![]() �cƽ��
�cƽ��![]() ���ɵĽ�.
���ɵĽ�.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com