【題目】橢圓
（
）的離心率是
，點
在短軸
上，且
。
（1）球橢圓
的方程；
（2）設
為坐標原點，過點
的動直線與橢圓交于
兩點。是否存在常數
，使得
為定值？若存在，求
的值；若不存在，請說明理由。
【答案】（1）
；（2）見解析.
【解析】（Ⅰ）由已知，點C，D的坐標分別為（0，－b），（0，b）
又點P的坐標為（0，1），且
＝－1
于是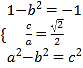
，解得a＝2，b＝
所以橢圓E方程為
.
（Ⅱ）當直線AB斜率存在時，設直線AB的方程為y＝kx＋1
A，B的坐標分別為（x1，y1），（x2，y2）
聯立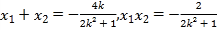
，得（2k2＋1）x2＋4kx－2＝0
其判別式△＝（4k）2＋8（2k2＋1）＞0
所以
從而
＝x1x2＋y1y2＋λ[x1x2＋（y1－1）（y2－1）]
＝（1＋λ）（1＋k2）x1x2＋k（x1＋x2）＋1
＝
＝－
所以，當λ＝1時，－＝－3
此時， 
＝－3為定值
當直線AB斜率不存在時，直線AB即為直線CD
此時
＝－2－1＝－3
故存在常數λ＝－1，使得
為定值－3.
各地期末復習特訓卷系列答案
小博士期末闖關100分系列答案
名校名師培優作業本加核心試卷系列答案科目：高中數學 來源： 題型：
【題目】供電部門對某社區1000位居民2017年12月份人均用電情況進行統計后，按人均用電量分為
五組，整理得到如下的頻率分布直方圖，則下列說法錯誤的是（ ）
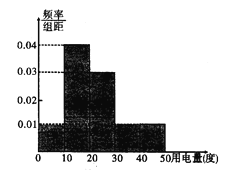
A. 12月份人均用電量人數最多的一組有400人
B. 12月份人均用電量不低于20度的有500人
C. 12月份人均用電量為25度
D. 在這1000位居民中任選1位協助收費，選到的居民用電量在
—組的概率為
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】橢圓
的離心率是
，過點
的動直線
與橢圓相交于
兩點，當直線
與
軸平行時，直線
被橢圓
截得的線段長為
.
（Ⅰ）求橢圓
的方程；
（Ⅱ）在
軸上是否存在異于點
的定點
，使得直線
變化時，總有
？若存在，求出點
的坐標；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】網格紙的各小格都是邊長為1的正方形，圖中粗實線畫出的是一個幾何體的三視圖，其中正視圖是正三角形，則該幾何體的外接球表面積為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在等腰梯形
中， 
， 
， 
，四邊形
為矩形，平面
平面
， 
.
（1）求證： 
平面
；
（2）點
在線段
上運動，設平面
與平面
所成二面角的平面角為
，試求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】一個正整數，若它的每個質因數都至少是兩重的（即每個質因數乘方次數都不小于2），則稱該正整數為“漂亮數”.相鄰兩個正整數皆為“漂亮數”，就稱它們是一對“孿生漂亮數”.例如8與9就是一對“孿生漂亮數”.請你再找出兩對“孿生漂亮數”來.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數f（x）=|x+1|+|x﹣3|
（1）求函數f（x）的最小值；
（2）若{x|f（x）≤t2﹣3t}∩{x|﹣2≤x≤0}≠．求實數t的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知F1 ， F2分別是橢圓 
的左、右焦點F1 ， F2關于直線x+y﹣2=0的對稱點是圓C的一條直徑的兩個端點．
（1）求圓C的方程；
（2）設過點F2的直線l被橢圓E和圓C所截得的弦長分別為a，b．當ab最大時，求直線l的方程．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
