
【題目】已知橢圓![]() 的左,右焦點分別為
的左,右焦點分別為![]() .過原點
.過原點![]() 的直線
的直線![]() 與橢圓交于
與橢圓交于![]() 兩點,點
兩點,點![]() 是橢圓
是橢圓![]() 上的點,若
上的點,若![]() ,
, ![]() ,且
,且![]() 的周長為
的周長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2) 設橢圓在點![]() 處的切線記為直線
處的切線記為直線![]() ,點
,點![]() 在
在![]() 上的射影分別為
上的射影分別為![]() ,過
,過![]() 作
作![]() 的垂線交
的垂線交![]() 軸于點
軸于點![]() ,試問
,試問![]() 是否為定值?若是,求出該定值;若不是,請說明理由.
是否為定值?若是,求出該定值;若不是,請說明理由.
【答案】(1) ![]() ;(2)1.
;(2)1.
【解析】試題分析; (1)設![]() ,則
,則![]() ,∴
,∴ ![]() ,設
,設![]() ,
, ![]() ,以及
,以及![]() ,
, ![]() ,由
,由![]() ,由橢圓的定義可得
,由橢圓的定義可得![]() ,結合
,結合![]() ,綜合
,綜合![]() 可得:
可得: ![]() ,可得橢圓
,可得橢圓![]() 的方程;
的方程;
(2)由(1)知![]() ,直線
,直線![]() 的方程為:
的方程為: ![]() ,由此可得
,由此可得
![]() .,又∵
.,又∵![]() ,∴
,∴ ![]() 的方程為
的方程為![]() ,可得
,可得![]()
則可得![]() ,又
,又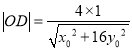 ,∴
,∴ ![]() .,故
.,故![]() .
.
當直線![]() 平行于
平行于![]() 軸時,易知
軸時,易知![]() ,結論顯然成立.
,結論顯然成立.
綜上,可知![]() 為定值1.
為定值1.
試題解析:(1)設![]() ,則
,則![]() ,∴
,∴![]() ,設
,設![]() ,由
,由![]() ,
,
![]() ,將
,將![]() 代入
代入![]() ,整體消元得:
,整體消元得:
![]() ,∴
,∴![]()
由![]() ,且
,且 ![]() ,∴
,∴ ![]() ,
,
由橢圓的對稱性知![]() ,
,
有![]() ,則
,則![]()
∵![]() ,綜合
,綜合![]() 可得:
可得: ![]()
∴橢圓![]() 的方程為:
的方程為: ![]() .
.
(2)由(1)知,直線![]() 的方程為:
的方程為: ![]()
即: ![]() ,所以
,所以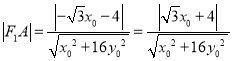
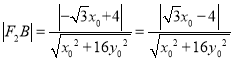
∴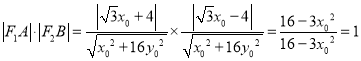 .
.
∵![]() ,∴
,∴ ![]() 的方程為
的方程為![]() ,令
,令![]() ,可得
,可得![]() ,∴
,∴ ![]()
則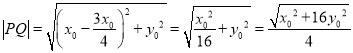
又點![]() 到直線
到直線![]() 的距離為
的距離為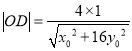 ,∴
,∴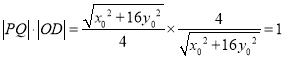 .
.
∴![]() .
.
當直線![]() 平行于
平行于![]() 軸時,易知
軸時,易知![]() ,結論顯然成立.
,結論顯然成立.
綜上, ![]() .
.


科目:高中數學 來源: 題型:
【題目】已知數列{an}是各項均不為0的等差數列.Sn為其前n項和,且滿足an2=S2n﹣1(n∈N*),bn=an2+λan , 若{bn}為遞增數列,則實數λ的范圍為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線l:ax﹣y+1=0與x軸,y軸分別交于點A,B.
(1)若a>0,點M(1,﹣1),點N(1,4),且以MN為直徑的圓過點A,求以AN為直徑的圓的方程;
(2)以線段AB為邊在第一象限作等邊三角形ABC,若a=﹣ ![]() ,且點P(m,
,且點P(m, ![]() )(m>0)滿足△ABC與△ABP的面積相等,求m的值.
)(m>0)滿足△ABC與△ABP的面積相等,求m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠有一批貨物由海上從甲地運往乙地,已知輪船的最大航行速度為60海里/小時,甲地至乙地之間的海上航行距離為600海里,每小時的運輸成本由燃料費和其它費用組成,輪船每小時的燃料費與輪船速度的平方成正比,比例系數為0.5,其它費用為每小時1250元.
(1)請把全程運輸成本![]() (元)表示為速度
(元)表示為速度![]() (海里/小時)的函數,并指明定義域;
(海里/小時)的函數,并指明定義域;
(2)為使全程運輸成本最小,輪船應以多大速度行駛?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() ,
,![]() ,函數
,函數![]() 的最大值為
的最大值為![]() .
.
(1)求![]() 的大小;
的大小;
(2)將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位,再將所得圖象上各點的橫坐標縮短為原來的
個單位,再將所得圖象上各點的橫坐標縮短為原來的![]() ,縱坐標不變,得到函數
,縱坐標不變,得到函數![]() 的圖象,作出函數
的圖象,作出函數![]() 在
在![]() 的圖象.
的圖象.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD﹣A1B1C1D1中,E是棱CC1的中點,F是側面BCC1B1內的動點,且A1F∥平面D1AE,則A1F與平面BCC1B1所成角的正切值t構成的集合是( ) 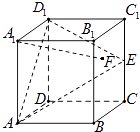
A.{t| ![]() }
}
B.{t| ![]() ≤t≤2}
≤t≤2}
C.{t|2 ![]() }
}
D.{t|2 ![]() }
}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設離心率為 ![]() 的橢圓
的橢圓![]() 的左、右焦點為
的左、右焦點為![]() , 點P是E上一點,
, 點P是E上一點, ![]() ,
, ![]() 內切圓的半徑為
內切圓的半徑為 ![]() .
.
(1)求E的方程;
(2)矩形ABCD的兩頂點C、D在直線![]() 上,A、B在橢圓E上,若矩形ABCD的周長為
上,A、B在橢圓E上,若矩形ABCD的周長為 ![]() , 求直線AB的方程.
, 求直線AB的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com