
【題目】在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)且
為參數(shù)且 ![]() )曲線
)曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù),且
為參數(shù),且![]() ),以
),以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線![]() 的極坐標(biāo)方程為:
的極坐標(biāo)方程為:![]() ,曲線
,曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求![]() 與
與![]() 的交點到極點的距離;
的交點到極點的距離;
(2)設(shè)![]() 與
與![]() 交于
交于![]() 點,
點,![]() 與
與![]() 交于
交于![]() 點,當(dāng)
點,當(dāng)![]() 在
在![]() 上變化時,求
上變化時,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1) 聯(lián)立曲線![]() 的極坐標(biāo)方程,求得交點極坐標(biāo)的極徑,由極徑的幾何意義即可得結(jié)果;(2)曲線
的極坐標(biāo)方程,求得交點極坐標(biāo)的極徑,由極徑的幾何意義即可得結(jié)果;(2)曲線![]() 的極坐標(biāo)方程與曲線
的極坐標(biāo)方程與曲線![]() 的極坐標(biāo)方程聯(lián)立得
的極坐標(biāo)方程聯(lián)立得![]() ,曲線
,曲線![]() 與曲線
與曲線![]() 的極坐標(biāo)方程聯(lián)立得
的極坐標(biāo)方程聯(lián)立得![]() ,
, ![]() ,利用輔助角公式與三角函數(shù)的有界性可得結(jié)果.
,利用輔助角公式與三角函數(shù)的有界性可得結(jié)果.
(1)聯(lián)立曲線![]() 的極坐標(biāo)方程
的極坐標(biāo)方程 得:
得: ![]() ,解得
,解得![]() ,即交點到極點的距離為
,即交點到極點的距離為![]() .
.
(2)曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() ,
,
曲線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() 聯(lián)立得
聯(lián)立得![]()
即![]()
曲線![]() 與曲線
與曲線![]() 的極坐標(biāo)方程聯(lián)立得
的極坐標(biāo)方程聯(lián)立得![]() ,
,
即![]() ,
,
所以![]() ,其中的終邊經(jīng)過點
,其中的終邊經(jīng)過點![]() ,
,
當(dāng)![]() ,即
,即![]() 時,
時,![]() 取得最大值為
取得最大值為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】近年來,隨著“一帶一路”倡議的推進,中國與沿線國家旅游合作越來越密切,中國到“一帶一路”沿線國家的游客人也越來越多,如圖是2013-2018年中國到“一帶一路”沿線國家的游客人次情況,則下列說法正確的是( )
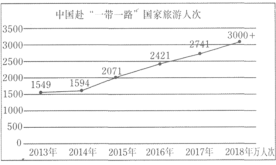
①2013-2018年中國到“一帶一路”沿線國家的游客人次逐年增加
②2013-2018年這6年中,2016年中國到“一帶一路”沿線國家的游客人次增幅最小
③2016-2018年這3年中,中國到“一帶一路”沿線國家的游客人次每年的增幅基本持平
A.①③B.②③C.①②D.①②③
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】橢圓![]() :
:![]()
![]() 的離心率為
的離心率為![]() ,拋物線
,拋物線![]() :
:![]() 截
截![]() 軸所得的線段長等于
軸所得的線段長等于![]() .
.![]() 與
與![]() 軸的交點為
軸的交點為![]() ,過點
,過點![]() 作直線
作直線![]() 與
與![]() 相交于點
相交于點![]() 直線
直線![]() 分別與
分別與![]() 相交于
相交于![]() .
.
(1)求證:![]() ;
;
(2)設(shè)![]() ,
,![]() 的面積分別為
的面積分別為![]() ,若
,若![]()
![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,一個鋁合金窗分為上、下兩欄,四周框架和中間隔檔的材料為鋁合金,寬均為6![]() ,上欄與下欄的框內(nèi)高度(不含鋁合金部分)的比為1:2,此鋁合金窗占用的墻面面積為28800
,上欄與下欄的框內(nèi)高度(不含鋁合金部分)的比為1:2,此鋁合金窗占用的墻面面積為28800![]() ,設(shè)該鋁合金窗的寬和高分別為
,設(shè)該鋁合金窗的寬和高分別為![]() ,鋁合金窗的透光部分的面積為
,鋁合金窗的透光部分的面積為![]() .
.
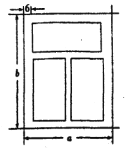
(1)試用![]() 表示
表示![]() ;
;
(2)若要使![]() 最大,則鋁合金窗的寬和高分別為多少?
最大,則鋁合金窗的寬和高分別為多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地區(qū)某農(nóng)產(chǎn)品近幾年的產(chǎn)量統(tǒng)計如表:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代碼 | 1 | 2 | 3 | 4 | 5 | 6 |
年產(chǎn)量 | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(1)根據(jù)表中數(shù)據(jù),建立![]() 關(guān)于
關(guān)于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
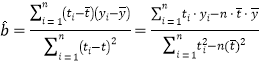 ,
,![]()
(2)若近幾年該農(nóng)產(chǎn)品每千克的價格![]() (單位:元)與年產(chǎn)量
(單位:元)與年產(chǎn)量![]() 滿足的函數(shù)關(guān)系式為
滿足的函數(shù)關(guān)系式為![]() ,且每年該農(nóng)產(chǎn)品都能售完.
,且每年該農(nóng)產(chǎn)品都能售完.
①根據(jù)(1)中所建立的回歸方程預(yù)測該地區(qū)2019(![]() )年該農(nóng)產(chǎn)品的產(chǎn)量;
)年該農(nóng)產(chǎn)品的產(chǎn)量;
②當(dāng)![]() 為何值時,銷售額
為何值時,銷售額![]() 最大?
最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() 恒成立,試確定實數(shù)
恒成立,試確定實數(shù)![]() 的取值范圍;
的取值范圍;
(3)證明![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形![]() 所在平面與半圓弧
所在平面與半圓弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上異于
上異于![]() ,
,![]() 的點.
的點.
(1)證明:平面![]() 平面
平面![]() ;
;
(2)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?說明理由.
?說明理由.

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 的最小正周期為
的最小正周期為![]() ,且點
,且點![]() 是該函數(shù)圖象的一個最高點.
是該函數(shù)圖象的一個最高點.
(1)求函數(shù)![]() 的解析式;
的解析式;
(2)求函數(shù)的單調(diào)增區(qū)間;
(3)若![]() ,求函數(shù)
,求函數(shù)![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某研究所計劃利用“神舟十一號”飛船進行新產(chǎn)品搭載實驗,計劃搭載新產(chǎn)品![]() ,要根據(jù)該產(chǎn)品的研制成本、產(chǎn)品質(zhì)量、搭載實驗費用和預(yù)計產(chǎn)生收益來決定具體安排,通過調(diào)查,搭載每件產(chǎn)品有關(guān)數(shù)據(jù)如表:
,要根據(jù)該產(chǎn)品的研制成本、產(chǎn)品質(zhì)量、搭載實驗費用和預(yù)計產(chǎn)生收益來決定具體安排,通過調(diào)查,搭載每件產(chǎn)品有關(guān)數(shù)據(jù)如表:
因素 | 產(chǎn)品 | 產(chǎn)品 | 備注 |
研制成本、搭載費用之和/萬元 | 20 | 30 | 計劃最大投資 |
金額300萬元產(chǎn)品質(zhì)量/千克 | 10 | 5 | 最大搭載 |
質(zhì)量110千克預(yù)計收益/萬元 | 80 | 60 | —— |
則使總預(yù)計收益達到最大時, ![]() 兩種產(chǎn)品的搭載件數(shù)分別為( )
兩種產(chǎn)品的搭載件數(shù)分別為( )
A. 9,4 B. 8,5 C. 9,5 D. 8,4
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com