
【題目】設(shè)等比數(shù)列{![]() }的公比為 q(q > 0,q = 1),前 n 項和為 Sn,且 2a1a3 = a4,數(shù)列{
}的公比為 q(q > 0,q = 1),前 n 項和為 Sn,且 2a1a3 = a4,數(shù)列{![]() }的前 n 項和 Tn 滿足2Tn = n(bn - 1),n ∈N*,b2 = 1.
}的前 n 項和 Tn 滿足2Tn = n(bn - 1),n ∈N*,b2 = 1.
(1) 求數(shù)列 {![]() },{
},{![]() }的通項公式;
}的通項公式;
(2) 是否存在常數(shù) t,使得 {Sn+ ![]() } 為等比數(shù)列?說明理由;
} 為等比數(shù)列?說明理由;
(3) 設(shè) cn =![]() ,對于任意給定的正整數(shù) k(k ≥2), 是否存在正整數(shù) l,m(k < l < m), 使得 ck,c1,cm 成等差數(shù)列?若存在,求出 l,m(用 k 表示),若不存在,說明理由.
,對于任意給定的正整數(shù) k(k ≥2), 是否存在正整數(shù) l,m(k < l < m), 使得 ck,c1,cm 成等差數(shù)列?若存在,求出 l,m(用 k 表示),若不存在,說明理由.
【答案】(1)![]() ; (2)存在
; (2)存在![]() ,使得
,使得![]() 是公比為
是公比為![]() 的等比數(shù)列;(3)存在
的等比數(shù)列;(3)存在![]() 符合題意.
符合題意.
【解析】
(1)利用基本量運算可得![]() ,利用n≥2時,2bn=2(Tn﹣Tn﹣1),整理可得
,利用n≥2時,2bn=2(Tn﹣Tn﹣1),整理可得![]() ;
;
(2)由Sn![]() ,分別討論t
,分別討論t![]() 時和t
時和t![]() 時,由等比數(shù)列的定義證明即可;
時,由等比數(shù)列的定義證明即可;
(3)假設(shè)對于任意給定的正整數(shù)k(k≥2),存在正整數(shù)l,m(k<l<m),使得ck,c1,cm成等差數(shù)列.則![]() ,整理得:2m+1
,整理得:2m+1![]() ,取l=2k,即可得解.
,取l=2k,即可得解.
(1)等比數(shù)列{an}的公比為q(q>0,q=1),∵2a1a3=a4,
∴![]() ,可得a1
,可得a1![]() .
.
∴an![]() qn﹣1
qn﹣1![]() .
.
數(shù)列{bn}的前n項和Tn滿足2Tn=n(bn﹣1),n∈N*,b2=1.
∴n≥2時,2bn=2(Tn﹣Tn﹣1)=n(bn﹣1)﹣(n﹣1)(bn﹣1﹣1),
化為:(n﹣2)bn=(n﹣1)bn﹣1+1,
當n≥3時,兩邊同除以(n﹣2)(n﹣1),可得:![]() ,
,
利用累加求和可得:![]() b2+1
b2+1![]() ,化為:bn=2n﹣3(n≥3),
,化為:bn=2n﹣3(n≥3),
當n=1時,2b1=b1﹣1,解得b1=﹣1,
經(jīng)過驗證n=1,2時也滿足.
∴bn=2n﹣3.
(2)由(1)可知:an![]() ,q>0,q≠1.
,q>0,q≠1.
∴Sn![]() .
.
①若t![]() 時,則Sn
時,則Sn![]() ,∴
,∴ q.
q.
即數(shù)列{Sn![]() }是公比為q的等比數(shù)列.
}是公比為q的等比數(shù)列.
②若t![]() 時,則Sn
時,則Sn![]() .
.
設(shè)![]() A,
A,![]() B.(其中A,B≠0).
B.(其中A,B≠0).
則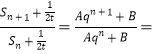 q
q![]() 不為常數(shù).
不為常數(shù).
綜上:存在t![]() 時,使得數(shù)列{Sn
時,使得數(shù)列{Sn![]() }是公比為q的等比數(shù)列.
}是公比為q的等比數(shù)列.
(3)由(1)可知:bn=2n﹣3.
![]() ,
,
假設(shè)對于任意給定的正整數(shù)k(k≥2),存在正整數(shù)l,m(k<l<m),使得ck,c1,cm成等差數(shù)列.
則![]() ,整理得:2m+1
,整理得:2m+1![]() ,
,
取l=2k,則2m+1=(4k+1)(2k+1),解得m=4k2+3k.
即存在l=2k,m=4k2+3k.符合題意.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應(yīng)用題系列答案
小學生10分鐘應(yīng)用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】在全面抗擊新冠肺炎疫情這一特殊時期,我市教育局提出“停課不停學”的口號,鼓勵學生線上學習.某校數(shù)學教師為了調(diào)查高三學生數(shù)學成績與線上學習時間之間的相關(guān)關(guān)系,在高三年級中隨機選取![]() 名學生進行跟蹤問卷,其中每周線上學習數(shù)學時間不少于
名學生進行跟蹤問卷,其中每周線上學習數(shù)學時間不少于![]() 小時的有
小時的有![]() 人,在這
人,在這![]() 人中分數(shù)不足
人中分數(shù)不足![]() 分的有
分的有![]() 人;在每周線上學習數(shù)學時間不足于
人;在每周線上學習數(shù)學時間不足于![]() 小時的人中,在檢測考試中數(shù)學平均成績不足
小時的人中,在檢測考試中數(shù)學平均成績不足![]() 分的占
分的占![]() .
.
(1)請完成![]() 列聯(lián)表;并判斷是否有
列聯(lián)表;并判斷是否有![]() 的把握認為“高三學生的數(shù)學成績與學生線上學習時間有關(guān)”;
的把握認為“高三學生的數(shù)學成績與學生線上學習時間有關(guān)”;
分數(shù)不少于 | 分數(shù)不足 | 合計 | |
線上學習時間不少于 | |||
線上學習時間不足 | |||
合計 |
(2)在上述樣本中從分數(shù)不足于![]() 分的學生中,按照分層抽樣的方法,抽到線上學習時間不少于
分的學生中,按照分層抽樣的方法,抽到線上學習時間不少于![]() 小時和線上學習時間不足
小時和線上學習時間不足![]() 小時的學生共
小時的學生共![]() 名,若在這
名,若在這![]() 名學生中隨機抽取
名學生中隨機抽取![]() 人,求這
人,求這![]() 人每周線上學習時間都不足
人每周線上學習時間都不足![]() 小時的概率.(臨界值表僅供參考)
小時的概率.(臨界值表僅供參考)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(參考公式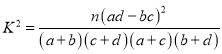 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知直線![]() :
: ![]() 與圓
與圓![]() 相交的弦長等于橢圓
相交的弦長等于橢圓![]() :
: ![]() (
(![]() )的焦距長.
)的焦距長.
(1)求橢圓![]() 的方程;
的方程;
(2)已知![]() 為原點,橢圓
為原點,橢圓![]() 與拋物線
與拋物線![]() (
(![]() )交于
)交于![]() 、
、![]() 兩點,點
兩點,點![]() 為橢圓
為橢圓![]() 上一動點,若直線
上一動點,若直線![]() 、
、![]() 與
與![]() 軸分別交于
軸分別交于![]() 、
、![]() 兩點,求證:
兩點,求證: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
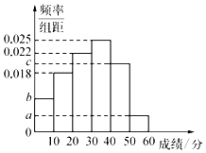
【題目】為調(diào)研高中生的作文水平.在某市普通高中的某次聯(lián)考中,參考的文科生與理科生人數(shù)之比為![]() ,且成績分布在
,且成績分布在![]() 的范圍內(nèi),規(guī)定分數(shù)在50以上(含50)的作文被評為“優(yōu)秀作文”,按文理科用分層抽樣的方法抽取400人的成績作為樣本,得到成績的頻率分布直方圖,如圖所示.其中
的范圍內(nèi),規(guī)定分數(shù)在50以上(含50)的作文被評為“優(yōu)秀作文”,按文理科用分層抽樣的方法抽取400人的成績作為樣本,得到成績的頻率分布直方圖,如圖所示.其中![]() 構(gòu)成以2為公比的等比數(shù)列.
構(gòu)成以2為公比的等比數(shù)列.
(1)求![]() 的值;
的值;
(2)填寫下面![]() 列聯(lián)表,能否在犯錯誤的概率不超過0.01的情況下認為“獲得優(yōu)秀作文”與“學生的文理科”有關(guān)?
列聯(lián)表,能否在犯錯誤的概率不超過0.01的情況下認為“獲得優(yōu)秀作文”與“學生的文理科”有關(guān)?
文科生 | 理科生 | 合計 | |
獲獎 | 6 | ||
不獲獎 | |||
合計 | 400 |
(3)將上述調(diào)查所得的頻率視為概率,現(xiàn)從全市參考學生中,任意抽取2名學生,記“獲得優(yōu)秀作文”的學生人數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學期望.
的分布列及數(shù)學期望.
附: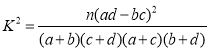 ,其中
,其中![]() .
.
| .15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某外賣企業(yè)兩位員工今年![]() 月某
月某![]() 天日派送外賣量的數(shù)據(jù)(單位:件),如莖葉圖所示針對這
天日派送外賣量的數(shù)據(jù)(單位:件),如莖葉圖所示針對這![]() 天的數(shù)據(jù),下面說法錯誤的是( )
天的數(shù)據(jù),下面說法錯誤的是( )
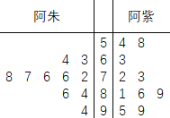
A.阿朱的日派送量的眾數(shù)為![]() B.阿紫的日派送量的中位數(shù)為
B.阿紫的日派送量的中位數(shù)為![]()
C.阿朱的日派送量的中位數(shù)為![]() D.阿朱的日派送外賣量更穩(wěn)定
D.阿朱的日派送外賣量更穩(wěn)定
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,設(shè)雙曲線![]() 的上焦點為
的上焦點為![]() ,上頂點為
,上頂點為![]() ,點
,點![]() 為雙曲線虛軸的左端點,已知
為雙曲線虛軸的左端點,已知![]() 的離心率為
的離心率為![]() ,且
,且![]() 的面積
的面積![]() .
.

(1)求雙曲線![]() 的方程;
的方程;
(2)設(shè)拋物線![]() 的頂點在坐標原點,焦點為
的頂點在坐標原點,焦點為![]() ,動直線
,動直線![]() 與
與![]() 相切于點
相切于點![]() ,與
,與![]() 的準線相交于點
的準線相交于點![]() ,試推斷以線段
,試推斷以線段![]() 為直徑的圓是否恒經(jīng)過
為直徑的圓是否恒經(jīng)過![]() 軸上的某個定點
軸上的某個定點![]() ?若是,求出定點
?若是,求出定點![]() 的坐標;若不是,請說明理由.
的坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】定義:對于任意![]() ,
,![]() 仍為數(shù)列
仍為數(shù)列![]() 中的項,則稱數(shù)列
中的項,則稱數(shù)列![]() 為“回歸數(shù)列”.
為“回歸數(shù)列”.
(1)己知![]() (
(![]() ),判斷數(shù)列
),判斷數(shù)列![]() 是否為“回歸數(shù)列”,并說明理由;
是否為“回歸數(shù)列”,并說明理由;
(2)若數(shù)列![]() 為“回歸數(shù)列”,
為“回歸數(shù)列”,![]() ,
,![]() ,且對于任意
,且對于任意![]() ,均有
,均有![]() 成立.①求數(shù)列
成立.①求數(shù)列![]() 的通項公式;②求所有的正整數(shù)s,t,使得等式
的通項公式;②求所有的正整數(shù)s,t,使得等式![]() 成立.
成立.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com