
設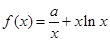 ,
,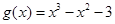 .
.
(Ⅰ)當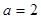 時,求曲線
時,求曲線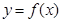 在
在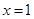 處的切線的方程;
處的切線的方程;
(Ⅱ)如果存在 ,使得
,使得 成立,求滿足上述條件的最大整數
成立,求滿足上述條件的最大整數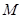 ;
;
(Ⅲ)如果對任意的 ,都有
,都有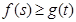 成立,求實數
成立,求實數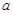 的取值范圍.
的取值范圍.
(1) ;(2)
;(2)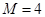 ;(3)
;(3)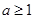 .
.
解析試題分析:本題考查導數的運算,利用導數研究函數的單調性、最值等基礎知識,考查函數思想和轉化思想,考查綜合分析和解決問題的能力.第一問,將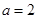 代入得到
代入得到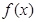 解析式,求
解析式,求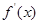 將
將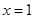 代入得到切線的斜率,再將
代入得到切線的斜率,再將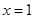 代入到
代入到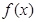 中得到切點的縱坐標,利用點斜式求出切線方程;第二問,先將問題轉化為
中得到切點的縱坐標,利用點斜式求出切線方程;第二問,先將問題轉化為 ,進一步轉化為求函數
,進一步轉化為求函數 的最大值和最小值問題,對
的最大值和最小值問題,對 求導,通過畫表判斷函數的單調性和極值,求出最值代入即可;第三問,結合第二問的結論,將問題轉化為
求導,通過畫表判斷函數的單調性和極值,求出最值代入即可;第三問,結合第二問的結論,將問題轉化為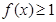 恒成立,進一步轉化為
恒成立,進一步轉化為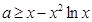 恒成立,設出新函數
恒成立,設出新函數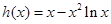 ,求
,求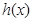 的最大值,所以
的最大值,所以 即可.
即可.
試題解析:(1)當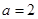 時,
時, ,
,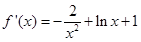 ,
,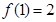 ,
,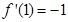 ,
,
所以曲線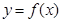 在
在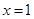 處的切線方程為
處的切線方程為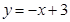 ; 2分
; 2分
(2)存在 ,使得
,使得 成立等價于:
成立等價于: ,
,
考察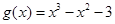 ,
, ,
,