
【題目】已知函數![]() .
.
(1)若函數f(x)的圖象在點(2,f(2))處的切線方程為9x﹣y+b=0,求實數a,b的值;
(2)若a≤0,求f(x)的單調減區間;
(3)對一切實數a∈(0,1),求f(x)的極小值的最大值.
【答案】(1)a=5.b=﹣15.(2)![]() ,(1,+∞).(3)
,(1,+∞).(3)![]() .
.
【解析】
(1)根據導數的幾何意義,即切線的斜率,待定系數即可求解;
(2)求導,對參數進行分類討論,利用導數判斷單調性即可;
(3)利用導數對函數單調性進行討論,求極小值關于![]() 的函數,再求函數的最大值即可.
的函數,再求函數的最大值即可.
(1)f′(x)=ax2﹣(a+1)x+1(a∈R),
由f′(2)=9,得a=5.
∴![]()
∴f(2)=3,
∴(2,3)在直線9x﹣y+b=0上,
∴b=﹣15.
(2)①若a=0,![]() ,
,
∴f(x)的單調減區間為(1,+∞).
②若a<0,則![]() ,
,
令f′(x)<0,得![]() .∴
.∴![]() ,或x>1.
,或x>1.
∴f(x)的單調減區間為![]() ,(1,+∞).
,(1,+∞).
(3)![]() ,0<a<1,
,0<a<1,
列表:
x | (﹣∞,1) | 1 | (1, |
| ( |
f′(x) | + | 0 | ﹣ | 0 | + |
f(x) | ↗ | 極大值 | ↘ | 極小值 | ↗ |
由圖可知:
f(x)的極小值為![]()
![]() .
.
當![]() 時,函數f(x)的極小值f(
時,函數f(x)的極小值f(![]() )取得最大值為
)取得最大值為![]() .
.
故函數f(x)的極小值f(![]() )取得最大值為
)取得最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,在直三棱柱![]() 中,
中,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,點D是側棱
,點D是側棱![]() 上的一點.
上的一點.
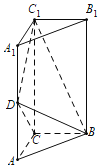
(1)證明:當點D是![]() 的中點時,
的中點時,![]() 平面BCD;
平面BCD;
(2)若二面角![]() 的余弦值為
的余弦值為![]() 求二面角
求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,是一塊半徑為4米的圓形鐵皮,現打算利用這塊鐵皮做一個圓柱形油桶.具體做法是從![]() 中剪裁出兩塊全等的圓形鐵皮
中剪裁出兩塊全等的圓形鐵皮![]() 與
與![]() 做圓柱的底面,剪裁出一個矩形
做圓柱的底面,剪裁出一個矩形![]() 做圓柱的側面(接縫忽略不計),
做圓柱的側面(接縫忽略不計),![]() 為圓柱的一條母線,點
為圓柱的一條母線,點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 的一條直徑上,
的一條直徑上,![]() ,
,![]() 分別與直線
分別與直線![]() 、
、![]() 相切,都與
相切,都與![]() 內切.
內切.
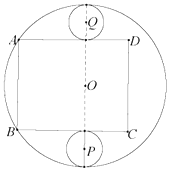
(1)求圓形鐵皮![]() 半徑的取值范圍;
半徑的取值范圍;
(2)請確定圓形鐵皮![]() 與
與![]() 半徑的值,使得油桶的體積最大.(不取近似值)
半徑的值,使得油桶的體積最大.(不取近似值)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將一顆骰子投擲兩次,第一次出現的點數記為a,第二次出現的點數記為b,設兩條直線l1:ax+by=2與l2:x+2y=2平行的概率為P1,相交的概率為P2,則點P(36P1,36P2)與圓C:x2+y2=1 098的位置關系是______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學大學畢業后,決定利用所學專業進行自主創業,經過市場調查,生產一小型電子產品需投入固定成本2萬元,每生產x萬件,需另投入流動成本C(x)萬元,當年產量小于7萬件時,C(x)=![]() x2+2x(萬元);當年產量不小于7萬件時,C(x)=6x+1nx+
x2+2x(萬元);當年產量不小于7萬件時,C(x)=6x+1nx+![]() ﹣17(萬元).已知每件產品售價為6元,假若該同學生產的產M當年全部售完.
﹣17(萬元).已知每件產品售價為6元,假若該同學生產的產M當年全部售完.
(1)寫出年利潤P(x)(萬元)關于年產量x(萬件)的函數解析式;(注:年利潤=年銷售收人﹣固定成本﹣流動成本
(2)當年產量約為多少萬件時,該同學的這一產品所獲年利潤最大?最大年利潤是多少?(取e3≈20)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“干支紀年法”是中國歷法上自古以來使用的紀年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被稱為“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”.“天干”以“甲”字開始,“地支”以“子”字開始,兩者按干支順序相配,組成了干支紀年法,其相配順序為:甲子、乙丑、丙寅、…、癸酉,甲戌、乙亥、丙子、…、癸未,甲申、乙酉、丙戌、…、癸巳,…,共得到60個組合,周而復始,循環記錄.2010年是“干支紀年法”中的庚寅年,那么2020年是“干支紀年法”中的( )
A.已亥年B.戊戌年C.庚子年D.辛丑年
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別是
的左、右焦點分別是![]() ,
,![]() ,點
,點![]() ,若
,若![]() 的內切圓的半徑與外接圓的半徑的比是
的內切圓的半徑與外接圓的半徑的比是![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設![]() 為橢圓
為橢圓![]() 的右頂點,設圓
的右頂點,設圓![]() :
:![]() ,不與
,不與![]() 軸垂直的直線
軸垂直的直線![]() 與
與![]() 交于
交于![]() 、
、![]() 兩點,原點
兩點,原點![]() 到直線
到直線![]() 的距離為
的距離為![]() ,線段
,線段![]() 、
、![]() 分別與橢圓
分別與橢圓![]() 交于
交于![]() 、
、![]() ,
,![]() ,垂足為
,垂足為![]() .設
.設![]() ,
,![]() ,
,![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() .
.
①試確定![]() 與
與![]() 的關系式;、
的關系式;、
②求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com