
【題目】已知![]() 為銳角
為銳角![]() 的外心,且三邊
的外心,且三邊![]() 與面積
與面積![]() 滿足
滿足![]() ,若
,若![]() (其中
(其中![]() 是實數),則
是實數),則![]() 的最大值是( )
的最大值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
利用余弦定理以及三角形的面積公式求出![]() ,以
,以![]() 邊所在的直線為
邊所在的直線為![]() 軸,
軸,![]() 邊的垂直平分線為
邊的垂直平分線為![]() 軸建立直角坐標系(
軸建立直角坐標系(![]() 為
為![]() 邊的中點),由外接圓的性質可得
邊的中點),由外接圓的性質可得![]() ,由
,由![]() ,不妨設外接圓的半徑
,不妨設外接圓的半徑![]() ,則
,則![]() ,可得
,可得![]() 的坐標,設
的坐標,設![]() ,則
,則![]() 的外接圓的方程為:
的外接圓的方程為:![]() ,利用向量的坐標運算可得
,利用向量的坐標運算可得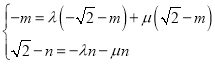 ,從而求出
,從而求出![]() ,代入外接圓方程可得
,代入外接圓方程可得![]() ,再利用基本不等式即可求解.
,再利用基本不等式即可求解.
由![]() ,可知
,可知![]() ,
,
解得![]() ,所以
,所以![]() ,
,
如圖所示,以![]() 邊所在的直線為
邊所在的直線為![]() 軸,
軸,![]() 邊的垂直平分線為
邊的垂直平分線為![]() 軸建立直角坐標系
軸建立直角坐標系
(![]() 為
為![]() 邊的中點)
邊的中點)
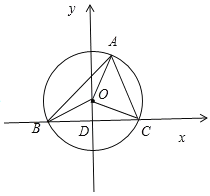
由外接圓的性質可得![]() ,
,
由![]() ,不妨設外接圓的半徑
,不妨設外接圓的半徑![]() ,
,
則![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
則![]() 的外接圓的方程為:
的外接圓的方程為:![]() ,
,
![]() ,
,
![]() ,
,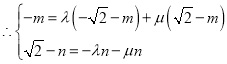 ,
,
![]() ,否則
,否則![]() 三點共線,由圖可知不可能的.
三點共線,由圖可知不可能的.
![]() 可化為
可化為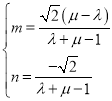 ,代入
,代入![]() 的外接圓的方程可得
的外接圓的方程可得
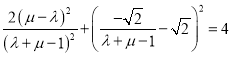 ,
,
化為![]() ,
,
化為![]() ,
,
解得![]() 或
或![]() ,
,
又![]() ,所以
,所以![]() ,
,
所以![]() 的最大值為
的最大值為![]() .
.
故選:D


科目:高中數學 來源: 題型:
【題目】古希臘時期,人們認為最美人體的頭頂至肚臍的長度與肚臍至足底的長度之比是![]() (
(![]() ≈0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是
≈0.618,稱為黃金分割比例),著名的“斷臂維納斯”便是如此.此外,最美人體的頭頂至咽喉的長度與咽喉至肚臍的長度之比也是![]() .若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26 cm,則其身高可能是
.若某人滿足上述兩個黃金分割比例,且腿長為105cm,頭頂至脖子下端的長度為26 cm,則其身高可能是

A. 165 cmB. 175 cmC. 185 cmD. 190cm
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為配合“2019雙十二”促銷活動,某公司的四個商品派送點如圖環形分布,并且公司給![]() 四個派送點準備某種商品各50個.根據平臺數據中心統計發現,需要將發送給
四個派送點準備某種商品各50個.根據平臺數據中心統計發現,需要將發送給![]() 四個派送點的商品數調整為40,45,54,61,但調整只能在相鄰派送點進行,每次調動可以調整1件商品.為完成調整,則( )
四個派送點的商品數調整為40,45,54,61,但調整只能在相鄰派送點進行,每次調動可以調整1件商品.為完成調整,則( )
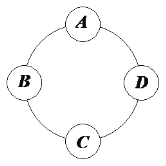
A.最少需要16次調動,有2種可行方案
B.最少需要15次調動,有1種可行方案
C.最少需要16次調動,有1種可行方案
D.最少需要15次調動,有2種可行方案
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,楔形幾何體![]() 由一個三棱柱截去部分后所得,底面
由一個三棱柱截去部分后所得,底面![]() 側面
側面![]() ,
,![]() ,楔面
,楔面![]() 是邊長為2的正三角形,點
是邊長為2的正三角形,點![]() 在側面
在側面![]() 的射影是矩形
的射影是矩形![]() 的中心
的中心![]() ,點
,點![]() 在
在![]() 上,且
上,且![]()

(1)證明:![]() 平面
平面![]() ;
;
(2)求楔面![]() 與側面
與側面![]() 所成二面角的余弦值.
所成二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為了了解該校某年級學生的閱讀量(分鐘),隨機抽取了n名學生,調查他們一天的閱讀時間,統計結果下圖表所示:
組號 | 分組 | 男生 人數 | 男生人數占本 組人數的頻率 | 頻率分布直方圖 |
第1組 |
| 5 | 0.5 |
|
第2組 |
| 18 | 0.9 | |
第3組 |
| 24 | 0.8 | |
第4組 |
|
| 0.4 | |
第5組 |
| 3 | 0.2 |
(1)求出![]() 與
與![]() 的值;
的值;
(2)—天的閱時間不少于35分鐘稱為“喜好閱讀者”.根據以上數據,完成下面的![]() 列聯表,并回答能否在犯錯誤的概率不超過0.05的前提下認為“喜好閱讀者”與“性別”有關?
列聯表,并回答能否在犯錯誤的概率不超過0.05的前提下認為“喜好閱讀者”與“性別”有關?
喜好閱讀者 | 非喜好閱讀者 | 合計 | |
男生 | |||
女生 | |||
合計 |
附: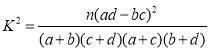 (其中
(其中![]() 為樣本容量).
為樣本容量).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com