
【題目】已知函數(shù)![]() 是定義在
是定義在![]() 的偶函數(shù),且
的偶函數(shù),且![]() .當(dāng)
.當(dāng)![]() 時,
時,![]() ,若方程
,若方程![]() 有300個不同的實數(shù)根,則實數(shù)m的取值范圍為( )
有300個不同的實數(shù)根,則實數(shù)m的取值范圍為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
首先由已知確定函數(shù)![]() 的周期是4,利用導(dǎo)數(shù)研究
的周期是4,利用導(dǎo)數(shù)研究![]() 在
在![]() 上的性質(zhì),單調(diào)性、極值,結(jié)合偶函數(shù)性質(zhì)作出
上的性質(zhì),單調(diào)性、極值,結(jié)合偶函數(shù)性質(zhì)作出![]() 在
在![]() 上的圖象,
上的圖象,![]() 的定義域是
的定義域是![]() 含有50個周期,方程
含有50個周期,方程![]() 有300個不同的實數(shù)根,那么在
有300個不同的實數(shù)根,那么在![]() 的一個周期內(nèi)有6個根,令
的一個周期內(nèi)有6個根,令![]() ,可知方程
,可知方程![]() 有兩個不等實根
有兩個不等實根![]() ,且
,且![]() ,
,![]() ,由二次方程根的分布知識可得解.
,由二次方程根的分布知識可得解.
由![]() 知函數(shù)的周期為4,當(dāng)
知函數(shù)的周期為4,當(dāng)![]() 時,
時,![]() ,則
,則![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ,
,![]() 遞減,當(dāng)
遞減,當(dāng)![]() 時,
時,![]() ,
,![]() 遞增,
遞增,![]() ,又
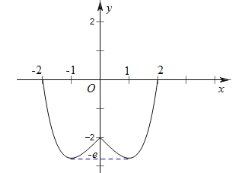
,又![]() 是偶函數(shù),作出
是偶函數(shù),作出![]() 在
在![]() 上的圖象,如圖.
上的圖象,如圖.
函數(shù)![]() 的周期是4,定義域為
的周期是4,定義域為![]() ,含有50個周期,
,含有50個周期,
方程![]() 有300個不同的實數(shù)根,因此在一個周期內(nèi)有6個根(這里
有300個不同的實數(shù)根,因此在一個周期內(nèi)有6個根(這里![]() ,
,![]() 不是方程的根).
不是方程的根).
令![]() ,方程
,方程![]() 有兩個不等實根
有兩個不等實根![]() ,且
,且![]() ,
,![]() ,設(shè)
,設(shè)![]() ,則
,則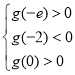 ,解得
,解得![]() .
.
故選:A.


 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖所示為一名曰“塹堵”的幾何體,已知 AE⊥底面BCFE , DF ∥ AE , DF = AE = 1, CE =![]() ,四邊形ABCD 是正方形.
,四邊形ABCD 是正方形.
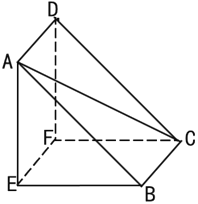
(1)《九章算術(shù)》中將四個面都是直角三角形的四面體稱為鱉臑.判斷四面體 EABC 是否為鱉臑,若是,寫出其 每一個面的直角,并證明;若不是,請說明理由.
(2)求四面體 EABC 的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)已知![]() 且
且![]() ,若函數(shù)
,若函數(shù)![]() 沒有零點,求證:
沒有零點,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 的圖像關(guān)于坐標原點對稱.
的圖像關(guān)于坐標原點對稱.
(1)求![]() 的值;
的值;
(2)若函數(shù)![]() 在
在![]() 內(nèi)存在零點,求實數(shù)
內(nèi)存在零點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)設(shè)![]() ,若不等式
,若不等式![]() 在
在![]() 上恒成立,求滿足條件的最小整數(shù)
上恒成立,求滿足條件的最小整數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】關(guān)于函數(shù)![]() 有下述四個結(jié)論:①若
有下述四個結(jié)論:①若![]() ,則
,則![]() ;②
;②![]() 的圖象關(guān)于點
的圖象關(guān)于點![]() 對稱;③函數(shù)
對稱;③函數(shù)![]() 在
在![]() 上單調(diào)遞增;④
上單調(diào)遞增;④![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后所得圖象關(guān)于
個單位長度后所得圖象關(guān)于![]() 軸對稱.其中所有正確結(jié)論的編號是( )
軸對稱.其中所有正確結(jié)論的編號是( )
A.①②④B.①②C.③④D.②④
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】若數(shù)列![]() 的每一項都不等于零,且對于任意的
的每一項都不等于零,且對于任意的![]() ,都有
,都有![]() (
(![]() 為常數(shù)),則稱數(shù)列
為常數(shù)),則稱數(shù)列![]() 為“類等比數(shù)列”;已知數(shù)列
為“類等比數(shù)列”;已知數(shù)列![]() 滿足:
滿足:![]()
![]() ,對于任意的
,對于任意的![]() ,都有
,都有![]() ;
;
(1)求證:數(shù)列![]() 是“類等比數(shù)列”;
是“類等比數(shù)列”;
(2)若![]() 是單調(diào)遞減數(shù)列,求實數(shù)
是單調(diào)遞減數(shù)列,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項之積取最大值時
項之積取最大值時![]() 的值;
的值;
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知某產(chǎn)品的銷售額![]() 與廣告費用
與廣告費用![]() 之間的關(guān)系如下表:
之間的關(guān)系如下表:
| 0 | 1 | 2 | 3 | 4 |
| 10 | 15 |
| 30 | 35 |
若根據(jù)表中的數(shù)據(jù)用最小二乘法求得![]() 對
對![]() 的回歸直線方程為
的回歸直線方程為![]() ,則下列說法中錯誤的是( )
,則下列說法中錯誤的是( )
A.產(chǎn)品的銷售額與廣告費用成正相關(guān)
B.該回歸直線過點![]()
C.當(dāng)廣告費用為10萬元時,銷售額一定為74萬元
D.![]() 的值是20
的值是20
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知命題P:函數(shù)![]() 且|f(a)|<2,命題Q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0}且A∩B=,
且|f(a)|<2,命題Q:集合A={x|x2+(a+2)x+1=0,x∈R},B={x|x>0}且A∩B=,
(1)分別求命題P、Q為真命題時的實數(shù)a的取值范圍;
(2)當(dāng)實數(shù)a取何范圍時,命題P、Q中有且僅有一個為真命題;
(3)設(shè)P、Q皆為真時a的取值范圍為集合S,![]() ,若RTS,求m的取值范圍.
,若RTS,求m的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com