
【題目】已知直線![]() 、
、![]() 與曲線
與曲線![]() 分別相交于點
分別相交于點![]() 、
、![]() 和
和![]() 、
、![]() ,我們將四邊形
,我們將四邊形![]() 稱為曲線
稱為曲線![]() 的內接四邊形.
的內接四邊形.
(1)若直線![]() 和
和![]() 將單位圓
將單位圓![]() 分成長度相等的四段弧,求
分成長度相等的四段弧,求![]() 的值;
的值;
(2)若直線![]() ,
,![]() 與圓
與圓![]() 分別交于點
分別交于點![]() 、
、![]() 和
和![]() 、
、![]() ,求證:四邊形
,求證:四邊形![]() 為正方形;
為正方形;
(3)求證:橢圓![]() 的內接正方形有且只有一個,并求該內接正方形的面積.
的內接正方形有且只有一個,并求該內接正方形的面積.
【答案】(1)![]() (2)證明見解析 (3)證明見解析
(2)證明見解析 (3)證明見解析
【解析】
(1)根據直線分圓分成長度相等的四段弧,得到![]() ,利用點到直線的距離公式進行求解即可.
,利用點到直線的距離公式進行求解即可.
(2)根據直線與圓相交的位置關系,利用消元法轉化為一元二次方程,根據根與系數之間的關系進行證明即可;
(3)根據橢圓內接正方形的關系,轉化為一元二次方程,根據根與系數之間的關系進行證明即可.
解:(1)由于直線![]() 和
和![]() 將單位圓
將單位圓![]() 分成長度相等的四段弧,
分成長度相等的四段弧,
所以![]() ,
,
在等腰直角![]() 中,圓心
中,圓心![]() 到直線
到直線![]() 的距離為
的距離為![]() ,∴
,∴![]() ,
,
同理![]() ,∴
,∴![]() ;
;
(2)由題知,直線![]() ,
,![]() 關于原點對稱,因為圓
關于原點對稱,因為圓![]() 的圓心為原點
的圓心為原點![]() ,
,
所以![]() ,故四邊形
,故四邊形![]() 為平行四邊形.易知,
為平行四邊形.易知,![]() 點在對角線
點在對角線![]() ,
,![]() 上.
上.
聯立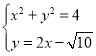 解得
解得![]() ,由
,由![]() ,
,![]() 得
得
![]()
![]() ,
,
所以![]() ,
,
于是![]() ,因為
,因為![]() ,所以四邊形
,所以四邊形![]() ABCD為正方形.
ABCD為正方形.
(3)證明:假設橢圓![]() 存在內接正方形,其四個頂點為
存在內接正方形,其四個頂點為![]() ,
,![]() ,
,![]() ,
,![]() .
.
當直線![]() 的斜率不存在時,設直線
的斜率不存在時,設直線![]() 、
、![]() 的方程為
的方程為![]() ,
,![]() ,因為
,因為![]() ,
,![]() ,
,![]() ,
,![]() 在橢圓上,
在橢圓上,
所以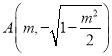 ,
,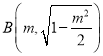 ,
,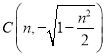 ,
,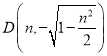 .
.
由四邊形![]() 為正方形,易知,
為正方形,易知,![]() ,
,![]() ,直線
,直線![]() 、
、![]() 的方程為
的方程為![]() ,
,![]() ,
,
正方形![]() 的面積
的面積![]() .
.
當直線![]() 的斜率存在時,設直線
的斜率存在時,設直線![]() 、
、![]() 的方程分別為
的方程分別為![]() ,
,![]() ,
,
顯然![]() .設
.設![]() ,
,![]() ,
,![]() ,
,![]() ,
,
聯立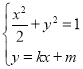 得
得![]() ,所以
,所以![]() ,
,![]()
代人![]() ,得
,得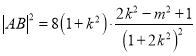 ,
,
同理可得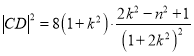 ,
,
因為![]() 為正方形,所以
為正方形,所以![]() 解得
解得![]()
因為![]() ,所以
,所以![]() ,
,
因此,直線![]() 與直線
與直線![]() 關于原點
關于原點![]() 對稱,
對稱,
所以原點![]() 為正方形的中心(由
為正方形的中心(由![]() 知
知![]() ,四邊形
,四邊形![]() 為平行四邊形
為平行四邊形
由![]() 為正方形知
為正方形知![]() ,
,
即![]()
代入得![]() ,解得
,解得![]() (注:此時四邊形
(注:此時四邊形![]() 為菱形)
為菱形)
由![]() 為正方形知
為正方形知![]() ,
,
因為直線![]() 與直線
與直線![]() 的距離為
的距離為![]() ,
,![]() ,故
,故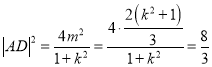
但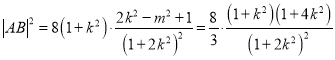 ,
,
由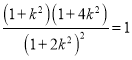 得
得![]() ,
,
∴![]() 即
即![]() ,與
,與![]() 矛盾.
矛盾.
所以![]() ,這與
,這與![]() 矛盾.
矛盾.
即當直線![]() 的斜率
的斜率![]() 存在時,橢圓內不存在正方形.
存在時,橢圓內不存在正方形.
綜上所述,橢圓![]() 的內接正方形有且只有一個,且其面積為
的內接正方形有且只有一個,且其面積為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】王老師是高三的班主任,為了在寒假更好的督促班上的學生完成學習作業,王老師特地組建了一個QQ群,群的成員由學生、家長、老師共同組成.已知該QQ群中男學生人數多于女學生人數,女學生人數多于家長人數,家長人數多于教師人數,教師人數的兩倍多于男學生人數.則該QQ群人數的最小值為( )
A.20B.22C.26D.28
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的兩個焦點
的兩個焦點![]() ,
,![]() 與短軸的一個端點構成一個等邊三角形,且直線
與短軸的一個端點構成一個等邊三角形,且直線![]() 與圓
與圓![]() 相切.
相切.
(1)求橢圓![]() 的方程;
的方程;
(2)已知過橢圓![]() 的左頂點
的左頂點![]() 的兩條直線
的兩條直線![]() ,
,![]() 分別交橢圓
分別交橢圓![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() ,求證:直線
,求證:直線![]() 過定點,并求出定點坐標;
過定點,并求出定點坐標;
(3)在(2)的條件下求![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某健身館在2019年7、8兩月推出優惠項目吸引了一批客戶.為預估2020年7、8兩月客戶投入的健身消費金額,健身館隨機抽樣統計了2019年7、8兩月100名客戶的消費金額,分組如下:![]() ,
,![]() ,
,![]() ,…,
,…,![]() (單位:元),得到如圖所示的頻率分布直方圖:
(單位:元),得到如圖所示的頻率分布直方圖:
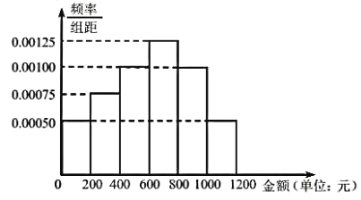
(1)請用抽樣的數據預估2020年7、8兩月健身客戶人均消費的金額(同一組中的數據用該組區間的中點值作代表);
(2)若把2019年7、8兩月健身消費金額不低于800元的客戶,稱為“健身達人”,經數據處理,現在列聯表中得到一定的相關數據,請補全空格處的數據,并根據列聯表判斷是否有![]() 的把握認為“健身達人”與性別有關?
的把握認為“健身達人”與性別有關?
健身達人 | 非健身達人 | 總計 | |
男 | 10 | ||
女 | 30 | ||
總計 |
(3)為吸引顧客,在健身項目之外,該健身館特別推出健身配套營養品的銷售,現有兩種促銷方案.
方案一:每滿800元可立減100元;
方案二:金額超過800元可抽獎三次,每次中獎的概率為![]() ,且每次抽獎互不影響,中獎1次打9折,中獎2次打8折,中獎3次打7折.
,且每次抽獎互不影響,中獎1次打9折,中獎2次打8折,中獎3次打7折.
若某人打算購買1000元的營養品,請從實際付款金額的數學期望的角度分析應該選擇哪種優惠方案.
附:
| 0.100 | 0.050 | 0.010 | 0.005 | |
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
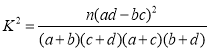
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題:“若![]() ,
,![]() 為異面直線,平面
為異面直線,平面![]() 過直線
過直線![]() 且與直線
且與直線![]() 平行,則直線
平行,則直線![]() 與平面
與平面![]() 的距離等于異面直線
的距離等于異面直線![]() ,
,![]() 之間的距離”為真命題.根據上述命題,若
之間的距離”為真命題.根據上述命題,若![]() ,
,![]() 為異面直線,且它們之間的距離為
為異面直線,且它們之間的距離為![]() ,則空間中與
,則空間中與![]() ,
,![]() 均異面且距離也均為
均異面且距離也均為![]() 的直線
的直線![]() 的條數為( )
的條數為( )
A.0條B.1條C.多于1條,但為有限條D.無數多條
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海水稻就是耐鹽堿水稻,是一種介于野生稻和栽培稻之間的普遍生長在海邊灘涂地區的水稻,具有抗旱抗澇、抗病蟲害、抗倒伏抗鹽堿等特點.近年來,我國的海水稻研究取得了階段性成果,目前已開展了全國大范圍試種.某農業科學研究所分別抽取了試驗田中的海水稻以及對照田中的普通水稻各![]() 株,測量了它們的根系深度(單位:
株,測量了它們的根系深度(單位:![]() ),得到了如下的莖葉圖,其中兩豎線之間表示根系深度的十位數,兩邊分別是海水稻和普通水稻根系深度的個位數,則下列結論中不正確的是( )
),得到了如下的莖葉圖,其中兩豎線之間表示根系深度的十位數,兩邊分別是海水稻和普通水稻根系深度的個位數,則下列結論中不正確的是( )
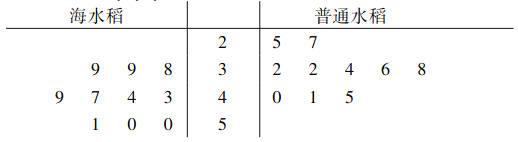
A.海水稻根系深度的中位數是![]()
B.普通水稻根系深度的眾數是![]()
C.海水稻根系深度的平均數大于普通水稻根系深度的平均數
D.普通水稻根系深度的方差小于海水稻根系深度的方差
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】提高過江大橋的車輛通行能力可改善整個城市的交通狀況,在一般情況下,大橋上的車流速度v(單位:千米/小時)是車流密度x(單位:輛/千米)的函數,當橋上的車流密度達到200輛/千米時,造成堵塞,此時車流速度為0;當車流密度不超過20輛/千米時,車流速度為60千米/小時,研究表明:當20≤x≤200時,車流速度v是車流密度x的一次函數.
(1)當0≤x≤200時,求函數v(x)的表達式;
(2)當車流密度x為多大時,車流量(單位時間內通過橋上某觀測點的車輛數,單位:輛/小時)f(x)=xv(x)可以達到最大,并求出最大值.(精確到1輛/小時).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 和
和![]() 是雙曲線
是雙曲線![]() 上的兩點,線段
上的兩點,線段![]() 的中點為
的中點為![]() ,直線
,直線![]() 不經過坐標原點
不經過坐標原點![]() .
.
(1)若直線![]() 和直線
和直線![]() 的斜率都存在且分別為
的斜率都存在且分別為![]() 和
和![]() ,求證:
,求證:![]() ;
;
(2)若雙曲線的焦點分別為![]() 、
、![]() ,點
,點![]() 的坐標為
的坐標為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,求由四點
,求由四點![]() 、
、![]() 、
、![]() 、
、![]() 所圍成四邊形
所圍成四邊形![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com