
(1)已知![]() ,求cosα﹣sinα的值;
,求cosα﹣sinα的值;
(2)當![]() ,k∈Z時,利用三角函數線表示出sinα,cosα,tanα并比較其大小.
,k∈Z時,利用三角函數線表示出sinα,cosα,tanα并比較其大小.
考點:
同角三角函數間的基本關系;三角函數線.
專題:
計算題;三角函數的求值.
分析:
(1)由![]() 可求得cos2α與sin2α,據α在第一象限角或第三象限角分類討論,即可求得cosα﹣sinα的值;
可求得cos2α與sin2α,據α在第一象限角或第三象限角分類討論,即可求得cosα﹣sinα的值;
(2)依題意,作出三角函數線表示出sinα,cosα,tanα,即可比較其大小.
解答:
解:(1)∵tanα=![]() =
=![]() ,可得α為第一象限角或第三象限角,…1分
,可得α為第一象限角或第三象限角,…1分
由![]() …2分
…2分
得:cos2α=![]() ,sin2α=
,sin2α=![]() …4分
…4分
①當α為第一象限角時,cosα=![]() ,sinα=
,sinα=![]() ,
,
故cosα﹣sinα=![]() …5分
…5分
②當α為第三象限角時,cosα=﹣![]() ,sinα=﹣
,sinα=﹣![]() ,
,
故cosα﹣sinα=![]() …6分
…6分
(2)如下圖所示
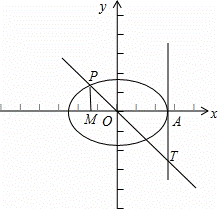
sinα,cosα,tanα分別用有向線段MP,OM,AT表示…10分
由三角函數線知sinα>cosα>tanα…12分
點評:
本題考查同角三角函數間的基本關系,突出分類討論思想與方程思想的考查,考查三角函數線,考查作圖能力,屬于中檔題.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:解答題
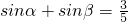
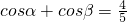 求cos(α-β)的值
求cos(α-β)的值查看答案和解析>>
科目:高中數學 來源:2012-2013學年山東省臨沂市郯城一中高一(下)4月月考數學試卷(解析版) 題型:解答題
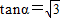 ,求cosα-sinα的值;
,求cosα-sinα的值; ,k∈Z時,利用三角函數線表示出sinα,cosα,tanα并比較其大小.
,k∈Z時,利用三角函數線表示出sinα,cosα,tanα并比較其大小.查看答案和解析>>
科目:高中數學 來源:2009-2010學年廣東省梅州市梅縣華僑中學高三(上)第三次月考數學試卷(理科)(解析版) 題型:解答題
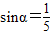 ,求cosα,tanα的值.
,求cosα,tanα的值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com