
【題目】為調(diào)查甲、乙兩校高三年級學生某次聯(lián)考數(shù)學成績情況,用簡單隨機抽樣,從這兩校中各抽取30名高三年級學生,以他們的數(shù)學成績(百分制)作為樣本,樣本數(shù)據(jù)的莖葉圖如圖.

(1)若甲校高三年級每位學生被抽取的概率為0.05,求甲校高三年級學生總?cè)藬?shù),并估計甲校高三年級這次聯(lián)考數(shù)學成績的及格率(60分及60分以上為及格);
(2)設(shè)甲、乙兩校高三年級學生這次聯(lián)考數(shù)學平均成績分別為![]() 1,
1,![]() 2,估計
2,估計![]() 1-
1-![]() 2的值.
2的值.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源: 題型:
【題目】脫貧是政府關(guān)注民生的重要任務,了解居民的實際收入狀況就顯得尤為重要.現(xiàn)從某地區(qū)隨機抽取![]() 個農(nóng)戶,考察每個農(nóng)戶的年收入與年積蓄的情況進行分析,設(shè)第
個農(nóng)戶,考察每個農(nóng)戶的年收入與年積蓄的情況進行分析,設(shè)第![]() 個農(nóng)戶的年收入
個農(nóng)戶的年收入![]() (萬元),年積蓄
(萬元),年積蓄![]() (萬元),經(jīng)過數(shù)據(jù)處理得
(萬元),經(jīng)過數(shù)據(jù)處理得![]()
(Ⅰ)已知家庭的年結(jié)余![]() 對年收入
對年收入![]() 具有線性相關(guān)關(guān)系,求線性回歸方程;
具有線性相關(guān)關(guān)系,求線性回歸方程;
(Ⅱ)若該地區(qū)的農(nóng)戶年積蓄在![]() 萬以上,即稱該農(nóng)戶已達小康生活,請預測農(nóng)戶達到小康生活的最低年收入應為多少萬元?
萬以上,即稱該農(nóng)戶已達小康生活,請預測農(nóng)戶達到小康生活的最低年收入應為多少萬元?
附:在![]() 中,
中, 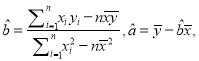 其中
其中![]() 為樣本平均值.
為樣本平均值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
已知曲線C的極坐標方程是![]() ,以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線L的參數(shù)方程是
,以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線L的參數(shù)方程是 (t為參數(shù)).
(t為參數(shù)).
(1)求曲線C的直角坐標方程和直線L的普通方程;
(2)設(shè)點P(m,0),若直線L與曲線C交于兩點A,B,且![]() ,求實數(shù)m的值.
,求實數(shù)m的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ).
).
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的零點;
的零點;
(2)求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)當![]() 時,若
時,若![]() 對
對![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
將圓![]() 上每一點的縱坐標保持不變,橫坐標變?yōu)樵瓉淼?/span>2倍得到曲線
上每一點的縱坐標保持不變,橫坐標變?yōu)樵瓉淼?/span>2倍得到曲線![]() .
.
(1)寫出曲線![]() 的參數(shù)方程;
的參數(shù)方程;
(2)以坐標原點為極點, ![]() 軸正半軸為極軸坐標建立極坐標系,已知直線
軸正半軸為極軸坐標建立極坐標系,已知直線![]() 的極坐標方程為
的極坐標方程為![]() ,若
,若![]() 分別為曲線
分別為曲線![]() 和直線
和直線![]() 上的一點,求
上的一點,求![]() 的最近距離.
的最近距離.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]() 過點
過點 ,且離心率為
,且離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若點![]() 與點
與點![]() 均在橢圓
均在橢圓![]() 上,且
上,且![]() 關(guān)于原點對稱,問:橢圓上是否存在點
關(guān)于原點對稱,問:橢圓上是否存在點![]() (點
(點![]() 在一象限),使得
在一象限),使得![]() 為等邊三角形?若存在,求出點
為等邊三角形?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為正方形,側(cè)面
為正方形,側(cè)面![]() 底面
底面![]() ,
,![]() 為
為![]() 中點,
中點,![]() .
.

(I)在線段![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() //平面
//平面![]() ,指出點
,指出點![]() 的位置并證明;
的位置并證明;
(II)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某煙花廠家為了測試最新研制出的一種“沖天”產(chǎn)品升空的安全性,特對其進行了一項測試。如圖,這種煙花在燃放點C進行燃放實驗,測試人員甲、乙分別在A,B兩地(假設(shè)三地在同一水平面上),測試人員甲測得A、B兩地相距80米且∠BAC=60°,甲聽到煙花燃放“沖天”時的聲音的時間比乙晚![]() 秒.在A地測得該煙花升至最高點H處的仰角為60°.(已知聲音的傳播速度為340米∕秒)
秒.在A地測得該煙花升至最高點H處的仰角為60°.(已知聲音的傳播速度為340米∕秒)
(1)求甲距燃放點C的距離;(2)求這種煙花的垂直“沖天”高度HC

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】隨著節(jié)假日外出旅游人數(shù)增多,倡導文明旅游的同時,生活垃圾處理也面臨新的挑戰(zhàn),某海濱城市沿海有![]() 三個旅游景點,在岸邊
三個旅游景點,在岸邊![]() 兩地的中點處設(shè)有一個垃圾回收站點
兩地的中點處設(shè)有一個垃圾回收站點![]() (如圖),
(如圖),![]() 兩地相距10
兩地相距10![]() ,從回收站
,從回收站![]() 觀望
觀望![]() 地和
地和![]() 地所成的視角為
地所成的視角為![]() ,且
,且![]() ,設(shè)
,設(shè)![]() ;
;
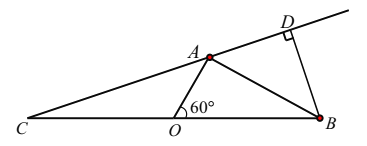
(1)用![]() 分別表示
分別表示![]() 和
和![]() ,并求出
,并求出![]() 的取值范圍;
的取值范圍;
(2)某一時刻太陽與![]() 三點在同一直線,此時
三點在同一直線,此時![]() 地到直線
地到直線![]() 的距離為
的距離為![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com