已知函數(shù)
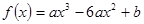
,問是否存在實數(shù)
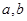
使
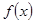
在
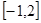
上取最大值3,最小值-29,若存在,求出
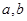
的值;不存在說明理由。
試題分析:顯然
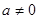
,
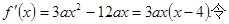
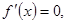
解得
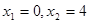
(舍去)
(1)當
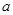
>0時,
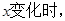
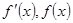
的變化情況如下:
所以當

時,
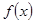
取得最大值,故
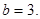
又
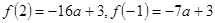
,
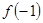
>
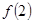
所以當
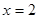
時,
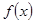
取得最小值,
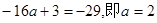
(2)當
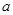
<0時,
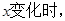
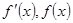
的變化情況如下:
所以當

時,
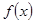
取得最小值,故
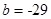
又
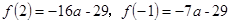
,
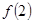
>
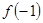
所以當
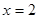
時,
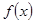
取得最大小值,
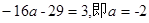
綜上所述
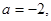
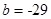
或
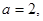
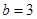
點評:典型題,在給定區(qū)間,導數(shù)值非負,函數(shù)是增函數(shù),導數(shù)值為非正,函數(shù)為減函數(shù)。求最值的步驟:計算導數(shù)、求駐點、討論駐點附近導數(shù)的正負、確定極值、計算得到函數(shù)值比較大小。本題利用“本解法”,直觀明了。
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
設(shè)函數(shù)

,且
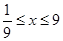
.
(1)求

的值;
(2)若令
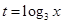
,求
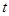
取值范圍;
(3)將
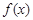
表示成以
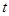
(
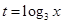
)為自變量的函數(shù),并由此,求函數(shù)
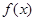
的最大值與最小值及與之對應(yīng)的
x的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若2
x-3
-x≥2
-y-3
y,則
| A.x-y≥0 | B.x-y≤0 | C.x+y≥0 | D.x+y≤0 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
函數(shù)y=2x4 -x2+1的遞減區(qū)間是
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
函數(shù)
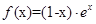
的單調(diào)遞減區(qū)間
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知f(x)是定義在(0,+
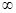
)上的非負可導函數(shù),且滿足
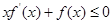
。對任意正數(shù)a、b,若a<b,則必有( )
| A.a(chǎn)f(b)≤bf(a) | B.bf(a)≤af(b) |
| C.a(chǎn)f(a)≤f(b) | D. bf(b)≤f(a) |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
函數(shù)
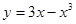
的單調(diào)遞增區(qū)間是
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
函數(shù)
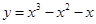
的單調(diào)遞增區(qū)間為______________ 遞減區(qū)間為____________
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知t為常數(shù),函數(shù)
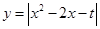
在區(qū)間[0,3]上的最大值為2,則t=_______。
查看答案和解析>>

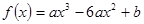 ,問是否存在實數(shù)
,問是否存在實數(shù)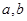 使
使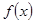 在
在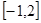 上取最大值3,最小值-29,若存在,求出
上取最大值3,最小值-29,若存在,求出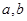 的值;不存在說明理由。
的值;不存在說明理由。 ,且
,且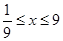 .
. 的值;
的值;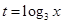 ,求
,求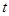 取值范圍;
取值范圍;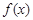 表示成以
表示成以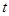 (
(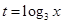 )為自變量的函數(shù),并由此,求函數(shù)
)為自變量的函數(shù),并由此,求函數(shù)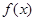 的最大值與最小值及與之對應(yīng)的x的值.
的最大值與最小值及與之對應(yīng)的x的值.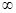 )上的非負可導函數(shù),且滿足
)上的非負可導函數(shù),且滿足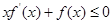 。對任意正數(shù)a、b,若a<b,則必有( )
。對任意正數(shù)a、b,若a<b,則必有( )