
如圖,四棱錐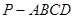 中,底面
中,底面 為梯形,
為梯形,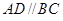 ,
,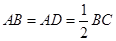 ,
, ,平面
,平面 平面
平面 ,
, .
.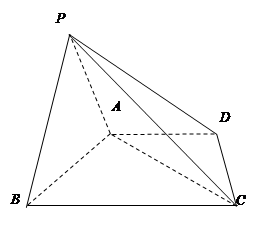
(1)求證: 平面
平面 ;
;
(2)求證: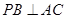 ;
;
(3)是否存在點 ,到四棱錐
,到四棱錐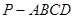 各頂點的距離都相等?并說明理由.
各頂點的距離都相等?并說明理由.
(1)參考解析;(2)參考解析;(3)存在
解析試題分析:(1)線面平面平行的證明,關鍵是在平面內找到一條直線與要證明的直線平行,根據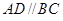 ,再根據直線BC,直線AD的位置關系,即可得線面平行.線面平行還有一種就是轉化為面面平行.線面平行的證明就是這兩種判斷的相互轉化.
,再根據直線BC,直線AD的位置關系,即可得線面平行.線面平行還有一種就是轉化為面面平行.線面平行的證明就是這兩種判斷的相互轉化.
(2)要證線線垂直轉化為線面垂直,由題意可知,通過證明直線AC垂直于平面PAB,由面面垂直可知,只需證明直線AC垂直于AB,在三角形ABC中,由所給條件即可得到AC垂直于AB.
(3)由(2)可知直線PB垂直于平面PAC.所以可得直線PB垂直于直線PC.通過三角形的BCD全等于三角形CBA,所以可得直線BD垂直于DC.所以BC是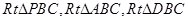 的斜邊,即BC的中點就是所要找的Q點.
的斜邊,即BC的中點就是所要找的Q點.
試題解析:(1)證明:底面 為梯形,
為梯形,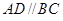 ,
,
又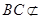 平面
平面 ,
,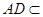 平面
平面 ,
,
所以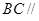 平面
平面 .
.
(2)證明:設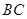 的中點為
的中點為 ,連結
,連結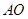 ,在梯形
,在梯形 中,
中,
因為 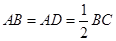 ,
, ,
,
所以 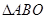 為等邊三角形,
為等邊三角形,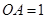 ,
,
又 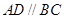 ,
,
所以 四邊形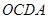 為菱形.
為菱形.
因為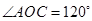 ,
,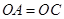 ,
,
所以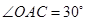 ,
,
所以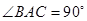 ,
,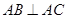 ,
,
又平面 平面
平面 ,
,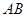 是交線,
是交線,
所以 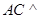 平面
平面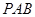 ,
,
所以 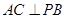 ,即
,即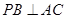 .
.
(3)解:因為 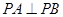 ,
,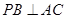 ,所以
,所以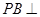 平面
平面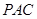 .
.
所以,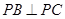 ,
,
所以 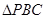 為直角三角形,
為直角三角形,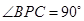 .
.
連結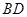 ,由(2)知
,由(2)知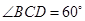 ,
,
所以 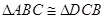 ,
,
所以 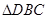 為直角三角形,
為直角三角形,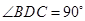 .
.
所以點 是三個直角三角形:
是三個直角三角形: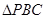 、
、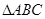 和
和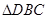 的共同的斜邊
的共同的斜邊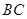 的中點,
的中點,
所以 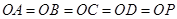 ,
,
所以存在點 (即點
(即點 )到四棱錐
)到四棱錐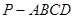 各頂點的距離都相等.
各頂點的距離都相等.
考點:1.線面平行的判定.2.線線垂直的判定.3.直角三形的性質.4.歸納推理論證的能力.


科目:高中數學 來源: 題型:解答題
已知A是△BCD平面外的一點,E,F分別是BC,AD的中點.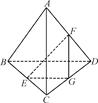
(1)求證:直線EF與BD是異面直線;
(2)若AC⊥BD,AC=BD,求EF與BD所成的角.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在長方體ABCD-A1B1C1D1中,底面A1B1C1D1是正方形,O是BD的中點,E是棱AA1上任意一點.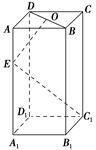
(1)證明:BD⊥EC1;
(2)如果AB=2,AE=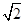 ,OE⊥EC1,求AA1的長.
,OE⊥EC1,求AA1的長.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,AB是圓O的直徑,PA垂直圓O所在的平面,C是圓O上的點.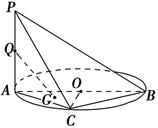
(1)求證:BC⊥平面PAC;
(2)設Q為PA的中點,G為△AOC的重心,求證:QG∥平面PBC.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在如圖所示的幾何體中,四邊形ABCD為正方形,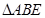 為直角三角形,
為直角三角形,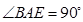 ,且
,且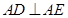 .
.
(1)證明:平面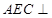 平面
平面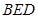 ;
;
(2)若AB=2AE,求異面直線BE與AC所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在三棱錐S—ABC中,SC⊥平面ABC,點P、M分別是SC和SB的中點,設PM=AC=1,∠ACB=90°,直線AM與直線SC所成的角為60°。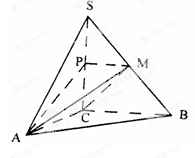
(1)求證:平面MAP⊥平面SAC。
(2)求二面角M—AC—B的平面角的正切值;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com