
【題目】通過隨機詢問110名性別不同的大學生是否愛好某項運動,得到如下的列聯表:
男 | 女 | 合計 | |
愛好 | 40 | 20 | 60 |
不愛好 | 20 | 30 | 50 |
合計 | 60 | 50 | 110 |
由K2=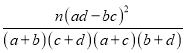 ,
,
附表:
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
參照附表,得到的正確結論是( )
A.在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別有關”
B.在犯錯誤的概率不超過0.1%的前提下,認為“愛好該項運動與性別無關”
C.有99%以上的把握認為“愛好該項運動與性別有關”
D.有99%以上的把握認為“愛好該項運動與性別無關”
 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源: 題型:
【題目】若在兩個成語中,一個成語的末字恰是另一成語的首字,則稱這兩個成語有頂真關系,現從分別貼有成語“人定勝天”、“爭先恐后”、“一馬當先”、“天馬行空”、“先發(fā)制人”的5張大小形狀完全相同卡片中,任意抽取2張,則這2張卡片上的成語有頂真關系的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班隨機抽查了![]() 名學生的數學成績,分數制成如圖的莖葉圖,其中
名學生的數學成績,分數制成如圖的莖葉圖,其中![]() 組學生每天學習數學時間不足
組學生每天學習數學時間不足![]() 個小時,
個小時,![]() 組學生每天學習數學時間達到一個小時,學校規(guī)定
組學生每天學習數學時間達到一個小時,學校規(guī)定![]() 分及
分及![]() 分以上記為優(yōu)秀,
分以上記為優(yōu)秀,![]() 分及
分及![]() 分以上記為達標,
分以上記為達標,![]() 分以下記為未達標.
分以下記為未達標.

(1)根據莖葉圖完成下面的列聯表:
達標 | 未達標 | 總計 | |
| |||
| |||
總計 |
(2)判斷是否有![]() 的把握認為“數學成績達標與否”與“每天學習數學時間能否達到一小時”有關.
的把握認為“數學成績達標與否”與“每天學習數學時間能否達到一小時”有關.
參考公式與臨界值表: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為鼓勵家校互動,與某手機通訊商合作,為教師辦理流量套餐.為了解該校教師手機流量使用情況,通過抽樣,得到![]() 位教師近
位教師近![]() 年每人手機月平均使用流量
年每人手機月平均使用流量![]() (單位:
(單位:![]() )的數據,其頻率分布直方圖如下:
)的數據,其頻率分布直方圖如下:

若將每位教師的手機月平均使用流量分別視為其手機月使用流量,并將頻率為概率,回答以下問題.
(Ⅰ) 從該校教師中隨機抽取![]() 人,求這
人,求這![]() 人中至多有
人中至多有![]() 人月使用流量不超過
人月使用流量不超過![]()
![]() 的概率;
的概率;
(Ⅱ) 現該通訊商推出三款流量套餐,詳情如下:
套餐名稱 | 月套餐費(單位:元) | 月套餐流量(單位: |
|
|
|
|
|
|
|
|
|
這三款套餐都有如下附加條款:套餐費月初一次性收取,手機使用一旦超出套餐流量,系統就自動幫用戶充值![]()
![]() 流量,資費
流量,資費![]() 元;如果又超出充值流量,系統就再次自動幫用戶充值
元;如果又超出充值流量,系統就再次自動幫用戶充值![]()
![]() 流量,資費
流量,資費![]() 元/次,依次類推,如果當月流量有剩余,系統將自動清零,無法轉入次月使用.
元/次,依次類推,如果當月流量有剩余,系統將自動清零,無法轉入次月使用.
學校欲訂購其中一款流量套餐,為教師支付月套餐費,并承擔系統自動充值的流量資費的![]() ,其余部分由教師個人承擔,問學校訂購哪一款套餐最經濟?說明理由.
,其余部分由教師個人承擔,問學校訂購哪一款套餐最經濟?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“割圓術”是劉徽最突出的數學成就之一,他在《九章算術注》中提出割圓術,并作為計算圓的周長,面積已經圓周率的基礎,劉徽把圓內接正多邊形的面積一直算到了正3072邊形,并由此而求得了圓周率為3.1415和3.1416這兩個近似數值,這個結果是當時世界上圓周率計算的最精確數據.如圖,當分割到圓內接正六邊形時,某同學利用計算機隨機模擬法向圓內隨機投擲點,計算得出該點落在正六邊形內的頻率為0.8269,那么通過該實驗計算出來的圓周率近似值為(參考數據:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區(qū)2007年至2013年農村居民家庭純收入y(單位:千元)的數據如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代號t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均純收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y關于t的線性回歸方程;
(2)利用(1)中的回歸方程,分析2007年至2013年該地區(qū)農村居民家庭人均純收入的變化情況,并預測該地區(qū)2015年農村居民家庭人均純收入.
附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
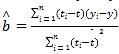 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的數表為“森德拉姆篩”(森德拉姆,東印度學者),其特點是每行每列都成等差數列.在此表中,數字“121”出現的次數為___________.
2 | 3 | 4 | 5 | 6 | 7 | …… |
3 | 5 | 7 | 9 | 11 | 13 | …… |
4 | 7 | 10 | 13 | 16 | 19 | …… |
5 | 9 | 13 | 17 | 21 | 25 | …… |
6 | 11 | 16 | 21 | 26 | 31 | …… |
7 | 13 | 19 | 25 | 31 | 37 | …… |
…… | …… | …… | …… | …… | …… | …… |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】
在極坐標系中,![]() 為極點,點
為極點,點![]() ,點
,點![]() .
.
(1)以極點為坐標原點,極軸為![]() 軸的正半軸建立平面直角坐標系,求經過
軸的正半軸建立平面直角坐標系,求經過![]() ,
,![]() ,
,![]() 三點的圓
三點的圓![]() 的直角坐標方程;
的直角坐標方程;
(2)在(1)的條件下,圓![]() 的極坐標方程為
的極坐標方程為![]() ,若圓
,若圓![]() 與圓
與圓![]() 相切,求實數
相切,求實數![]() 的值.
的值.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com