
【題目】在棱長為![]() 的正方體
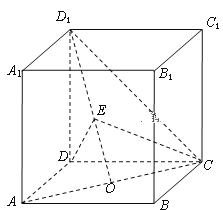
的正方體![]() 中,O是AC的中點,E是線段D1O上一點,且D1E=λEO.
中,O是AC的中點,E是線段D1O上一點,且D1E=λEO.
(1)若λ=1,求異面直線DE與CD1所成角的余弦值;
(2)若平面CDE⊥平面CD1O,求λ的值.
【答案】(1)![]() (2)λ=2
(2)λ=2
【解析】分析:以![]() 為單位正交基底建立如圖所示的空間直角坐標系
為單位正交基底建立如圖所示的空間直角坐標系![]() ,寫出各點的坐標,
,寫出各點的坐標,
(1)求出異面直線![]() 與
與![]() 1的方向向量用數量積公式兩線夾角的余弦值(或補角的余弦值)
1的方向向量用數量積公式兩線夾角的余弦值(或補角的余弦值)
(2)求出兩個平面的法向量,由于兩個平面垂直,故它們的法向量的內積為0,由此方程求參數![]() 的值即可.
的值即可.
詳解:
(1)以![]() 為單位正交基底建立如圖所示的空間直角坐標系
為單位正交基底建立如圖所示的空間直角坐標系![]() .
.
則A(1,0,0),![]() ,
,![]() ,D1(0,0,1),
,D1(0,0,1),
E![]() ,
,
于是![]() ,
,![]() .
.
由cos![]() =
=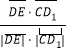 =
=![]() .
.
所以異面直線AE與CD1所成角的余弦值為![]() .
.
(2)設平面CD1O的向量為m=(x1,y1,z1),由m·![]() =0,m·
=0,m·![]() =0
=0
得  取x1=1,得y1=z1=1,即m=(1,1,1) . ………8分
取x1=1,得y1=z1=1,即m=(1,1,1) . ………8分
由D1E=λEO,則E![]() ,
,![]() =
=![]() .10分
.10分
又設平面CDE的法向量為n=(x2,y2,z2),由n·![]() =0,n·
=0,n·![]() =0.
=0.
得  取x2=2,得z2=-λ,即n=(-2,0,λ) .12分
取x2=2,得z2=-λ,即n=(-2,0,λ) .12分
因為平面CDE⊥平面CD1F,所以m·n=0,得![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】某地區現有一個直角梯形水產養殖區ABCD,∠ABC=90°,AB∥CD,AB=800m,BC=1600m,CD=4000m,在點P處有一燈塔(如圖),且點P到BC,CD的距離都是1200m,現擬將養殖區ACD分成兩塊,經過燈塔P增加一道分隔網EF,在△AEF內試驗養殖一種新的水產品,當△AEF的面積最小時,對原有水產品養殖的影響最小.設AE=d.
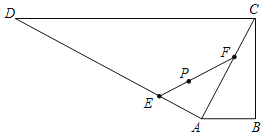
(1)若P是EF的中點,求d的值;
(2)求對原有水產品養殖的影響最小時的d的值,并求△AEF面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的正半軸,建立平面直角坐標系,直線
軸的正半軸,建立平面直角坐標系,直線![]() 過點
過點![]() ,傾斜角為
,傾斜角為![]() .
.
(1)求曲線![]() 的直角坐標方程與直線l的參數方程;
的直角坐標方程與直線l的參數方程;
(2)設直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x-lnx,g(x)=x2-ax.
(1)求函數f(x)在區間[t,t+1](t>0)上的最小值m(t);
(2)令h(x)=g(x)-f(x),A(x1,h(x1)),B(x2,h(x2))(x1≠x2)是函數h(x)圖像上任意兩點,且滿足![]() >1,求實數a的取值范圍;
>1,求實數a的取值范圍;
(3)若x∈(0,1],使f(x)≥![]() 成立,求實數a的最大值.
成立,求實數a的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=eax﹣x﹣1,且f(x)≥0.
(1)求a;
(2)在函數f(x)的圖象上取定兩點A(x1,f(x1)),B(x2,f(x2))(x1<x2),記直線AB的斜率為k,問:是否存在x0∈(x1,x2),使f'(x0)=k成立?若存在,求出x0的值(用x1,x2表示);若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某搜索引擎廣告按照付費價格對搜索結果進行排名,點擊一次付費價格排名越靠前,被點擊的次數也可能會提高,已知某關鍵詞被甲、乙等多個公司競爭,其中甲、乙付費情況與每小時點擊量結果繪制成如下的折線圖.
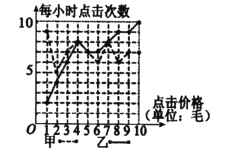
(1)試根據所給數據計算每小時點擊次數的均值方差并分析兩組數據的特征;
(2)若把乙公司設置的每次點擊價格為x,每小時點擊次數為y,則點(x,y)近似在一條直線附近.試根據前5次價格與每小時點擊次數的關系,求y關于x的回歸直線![]() .(附:回歸方程系數公式:
.(附:回歸方程系數公式: )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的點,
上的點,![]() 的面積最大值為
的面積最大值為![]() ,直線
,直線![]() 與
與![]() 交于
交于![]() 兩點,且
兩點,且![]() (
(![]() 為坐標原點)
為坐標原點)
(1)求橢圓![]() 的方程;
的方程;
(2)求證:![]() 到直線
到直線![]() 的距離為定值,并求其定值.
的距離為定值,并求其定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 指數是用體重公斤數除以身高米數的平方得出的數字,是國際上常用的衡量人體胖瘦程度以及是否健康的一個標準.對于高中男體育特長生而言,當
指數是用體重公斤數除以身高米數的平方得出的數字,是國際上常用的衡量人體胖瘦程度以及是否健康的一個標準.對于高中男體育特長生而言,當![]() 數值大于或等于20.5時,我們說體重較重,當
數值大于或等于20.5時,我們說體重較重,當![]() 數值小于20.5時,我們說體重較輕,身高大于或等于
數值小于20.5時,我們說體重較輕,身高大于或等于![]() 我們說身高較高,身高小于170cm我們說身高較矮.
我們說身高較高,身高小于170cm我們說身高較矮.
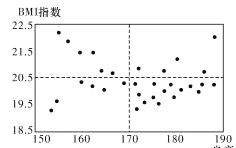
(1)已知某高中共有32名男體育特長生,其身高與![]() 指數的數據如散點圖,請根據所得信息,完成下述列聯表,并判斷是否有
指數的數據如散點圖,請根據所得信息,完成下述列聯表,并判斷是否有![]() 的把握認為男生的身高對
的把握認為男生的身高對![]() 指數有影響.
指數有影響.
身高較矮 | 身高較高 | 合計 | |
體重較輕 | |||
體重較重 | |||
合計 |
(2)①從上述32名男體育特長生中隨機選取8名,其身高和體重的數據如表所示:
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 166 | 167 | 160 | 173 | 178 | 169 | 158 | 173 |
體重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
根據最小二乘法的思想與公式求得線性回歸方程為![]() .利用已經求得的線性回歸方程,請完善下列殘差表,并求解釋變量(身高)對于預報變量(體重)變化的貢獻值(保留兩位有效數字)
.利用已經求得的線性回歸方程,請完善下列殘差表,并求解釋變量(身高)對于預報變量(體重)變化的貢獻值(保留兩位有效數字)![]() ;
;
編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
體重 | 57 | 58 | 53 | 61 | 66 | 57 | 50 | 66 |
殘差 | 0.1 | 0.3 | 0.9 |
|
|
②通過殘差分析,對于殘差的最大(絕對值)的那組數據,需要確認在樣本點的采集中是否有人為的錯誤,已知通過重新采集發現,該組數據的體重應該為![]() .請重新根據最最小二乘法的思想與公式,求出男體育特長生的身高與體重的線性回歸方程.
.請重新根據最最小二乘法的思想與公式,求出男體育特長生的身高與體重的線性回歸方程.
(參考公式)
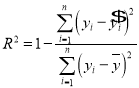 ,
,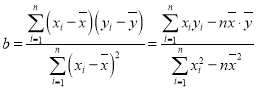 ,
,![]() ,
,![]() ,
,![]() .
.
(參考數據)
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
0.10
0.05
0.01
0.005
![]()
2.706
3.811
6.635
7.879
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com