
【題目】現有某種不透明充氣包裝的袋裝零食,每袋零食附贈玩具A,B,C中的一個.對某零售店售出的100袋零食中附贈的玩具類型進行追蹤調查,得到以下數據:
BBABC ACABA AAABC BABAA CAAAB
ABCCC BCBBC CABCA BACAB BCBCB
BCCCA BCCAA BCCCB ACCBB BACAB
ACCAB BBBAA CABCA BCBBC CABCA
(1)能否認為購買一袋該零食,獲得玩具A,B,C的概率相同?請說明理由;
(2)假設每袋零食隨機附贈玩具A,B,C是等可能的,某人一次性購買該零食3袋,求他能從這3袋零食中集齊玩具A,B及C的概率![]() .
.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)答案一:能.假設購買一袋該零食,獲得玩具A,B,C的概率相同,均為![]() ,由統計數據可得獲得玩具A,B,C的頻率分別是32%,35%,33%,與
,由統計數據可得獲得玩具A,B,C的頻率分別是32%,35%,33%,與![]() 非常接近,故可以認為題設成立;答案二:不能.從統計數據中得出獲得玩具A,B,C的頻率分別是32%,35%,33%,由
非常接近,故可以認為題設成立;答案二:不能.從統計數據中得出獲得玩具A,B,C的頻率分別是32%,35%,33%,由![]() ,可認為差別較大,題設不成立(二者言之有理即可);
,可認為差別較大,題設不成立(二者言之有理即可);
(2)將題中的基本事件全部列舉出來,再找出滿足條件的基本事件個數,最后根據古典概型的概率計算公式計算即可.
(1)答案一:能
假設購買一袋該零食,獲得玩具A,B,C的概率相同,
此時購買一袋該零食獲得每一款玩具的概率均為![]() .
.
對統計數據進行整理,可得購買一袋該零食,獲得玩具A,B,C的頻率分別是32%,35%,33%,
與假設中的概率非常接近,故可以認為假設成立,
即能夠認為購買一袋該零食,獲得玩具A,B,C的概率相同;
答案二:不能
對統計數據進行整理,可得購買一袋該零食,獲得玩具A,B,C的頻率分別是32%,35%,33%,
其中![]() ,差別較大,
,差別較大,
故不能夠認為購買一袋該零食,獲得玩具A,B,C的概率相同;
(二者言之有理即可).
(2)據題設知,將其購買的第一袋第二袋第三袋零食中附贈的玩具按順序列出,
可知共有27種不同的可能,列舉如下:
AAA AAB AAC ABA ABB ABC ACA ACB ACC
BAA BAB BAC BBA BBB BBC BCA BCB BCC
CAA CAB CAC CBA CBB CBC CCA CCB CCC
其中,可集齊三種玩具的情況共有6種(以下劃線形式標出),
而每種可能出現的機會相等,
根據古典概型的概率計算公式知![]() .
.


科目:高中數學 來源: 題型:
【題目】已知點![]() 為拋物線
為拋物線![]() 的焦點,點
的焦點,點![]() 在拋物線
在拋物線![]() 上,過點
上,過點![]() 的直線交拋物線
的直線交拋物線![]() 于
于![]() 兩點,線段
兩點,線段![]() 的中點為
的中點為![]() ,且滿足
,且滿足![]() .
.
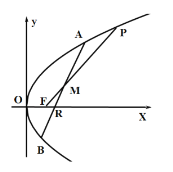
(1)若直線![]() 的斜率為1,求點
的斜率為1,求點![]() 的坐標;
的坐標;
(2)若![]() ,求四邊形
,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線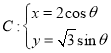 (
(![]() 為參數),以原點
為參數),以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程
的極坐標方程![]() ,點
,點![]() 在直線
在直線![]() 上,直線
上,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)求曲線![]() 的普通方程及直線
的普通方程及直線![]() 的參數方程;
的參數方程;
(2)求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,已知等邊![]() 的邊長為3,點
的邊長為3,點![]() ,
,![]() 分別是邊
分別是邊![]() ,
,![]() 上的點,且
上的點,且![]() ,
,![]() .如圖2,將
.如圖2,將![]() 沿
沿![]() 折起到
折起到![]() 的位置.
的位置.
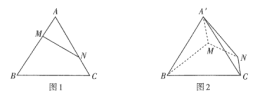
(1)求證:平面![]() 平面
平面![]() ;
;
(2)給出三個條件:①![]() ;②二面角
;②二面角![]() 大小為
大小為![]() ;③
;③![]() .在這三個條件中任選一個,補充在下面問題的條件中,并作答:在線段
.在這三個條件中任選一個,補充在下面問題的條件中,并作答:在線段![]() 上是否存在一點
上是否存在一點![]() ,使直線
,使直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,若存在,求出
,若存在,求出![]() 的長;若不存在,請說明理由.注:如果多個條件分別解答,按第一個解答給分
的長;若不存在,請說明理由.注:如果多個條件分別解答,按第一個解答給分
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x|+|x﹣1|.
(1)若f(x)≥|m﹣1|恒成立,求實數m的最大值M;
(2)在(1)成立的條件下,正實數a,b滿足a2+b2=M,證明:a+b≥2ab.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以平面直角坐標系![]() 的原點為極點,
的原點為極點,![]() 軸的非負半軸為極軸且取相同的單位長度建立極坐標系,已知過點
軸的非負半軸為極軸且取相同的單位長度建立極坐標系,已知過點![]() 且斜率為1的直線
且斜率為1的直線![]() 與曲線
與曲線![]() :
:![]() (
(![]() 是參數)交于
是參數)交于![]() 兩點,與直線
兩點,與直線![]() :
:![]() 交于點
交于點![]() .
.
(1)求曲線![]() 的普通方程與直線
的普通方程與直線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 的中點為
的中點為![]() ,比較
,比較![]() 與
與![]() 的大小關系,并說明理由.
的大小關系,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com