
【題目】如圖所示,在正方體![]() 中,
中,![]() 、
、![]() 分別為
分別為![]() 和
和![]() 的中點.
的中點.

(1)求證:![]() 平面
平面![]() ;
;
(2)求直線![]() 與面
與面![]() 所成的角的余弦值.
所成的角的余弦值.
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 的定義域是
的定義域是![]() 的一切實數(shù),對定義域內的任意
的一切實數(shù),對定義域內的任意![]() ,都有
,都有![]() 且當
且當![]() 時,
時,![]() .
.
(1)求證:![]() 是偶函數(shù);
是偶函數(shù);
(2)求證:![]() 在
在![]() 上是增函數(shù);
上是增函數(shù);
(3)試比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】口袋里裝有1紅,2白,3黃共6個形狀相同的小球,從中取出2球,事件![]() “取出的兩球同色”,
“取出的兩球同色”,![]() “取出的2球中至少有一個黃球”,
“取出的2球中至少有一個黃球”,![]() “取出的2球至少有一個白球”,
“取出的2球至少有一個白球”,![]() “取出的兩球不同色”,
“取出的兩球不同色”,![]() “取出的2球中至多有一個白球”.下列判斷中正確的序號為________.
“取出的2球中至多有一個白球”.下列判斷中正確的序號為________.
①![]() 與
與![]() 為對立事件;②
為對立事件;②![]() 與
與![]() 是互斥事件;③
是互斥事件;③![]() 與
與![]() 是對立事件:④
是對立事件:④![]() ;⑤
;⑤![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“活水圍網(wǎng)”養(yǎng)魚技術具有養(yǎng)殖密度高、經(jīng)濟效益好的特點.研究表明:“活水圍網(wǎng)”養(yǎng)魚時,某種魚在一定的條件下,每尾魚的平均生長速度![]() (單位:千克/年)是養(yǎng)殖密度
(單位:千克/年)是養(yǎng)殖密度![]() (單位:尾/立方米)的函數(shù).當
(單位:尾/立方米)的函數(shù).當![]() 時,
時,![]() 的值為2千克/年;當
的值為2千克/年;當![]() 時,
時,![]() 是
是![]() 的一次函數(shù);當
的一次函數(shù);當![]() 時,因缺氧等原因,
時,因缺氧等原因,![]() 的值為0千克/年.
的值為0千克/年.
(1)當![]() 時,求
時,求![]() 關于
關于![]() 的函數(shù)表達式.
的函數(shù)表達式.
(2)當養(yǎng)殖密度![]() 為多少時,魚的年生長量(單位:千克/立方米)可以達到最大?并求出最大值.
為多少時,魚的年生長量(單位:千克/立方米)可以達到最大?并求出最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
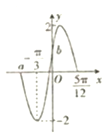
【題目】函數(shù)f(x)=Asin(2ωx+φ)(A>0,ω>0,|φ|<![]() )的部分圖象如圖所示
)的部分圖象如圖所示
(1)求A,ω,φ的值;
(2)求圖中a,b的值及函數(shù)f(x)的遞增區(qū)間;
(3)若α∈[0,π],且f(α)=![]() ,求α的值.
,求α的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某種計算機病毒是通過電子郵件進行傳播的,下表是某公司前5天監(jiān)測到的數(shù)據(jù):
第 | 1 | 2 | 3 | 4 | 5 |
被感染的計算機數(shù)量 | 10 | 20 | 39 | 81 | 160 |
則下列函數(shù)模型中,能較好地反映計算機在第![]() 天被感染的數(shù)量
天被感染的數(shù)量![]() 與
與![]() 之間的關系的是
之間的關系的是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 定義在
定義在![]() 上且滿足下列兩個條件:
上且滿足下列兩個條件:
①對任意![]() 都有
都有![]() ;
;
②當![]() 時,有
時,有![]() ,
,
(1)求![]() ,并證明函數(shù)
,并證明函數(shù)![]() 在
在![]() 上是奇函數(shù);
上是奇函數(shù);
(2)驗證函數(shù)![]() 是否滿足這些條件;
是否滿足這些條件;
(3)若![]() ,試求函數(shù)
,試求函數(shù)![]() 的零點.
的零點.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直線AB,且AB![]() BP
BP![]() 2,AD=AE=1,AE⊥AB,且AE∥BP.
2,AD=AE=1,AE⊥AB,且AE∥BP.

(1)求平面PCD與平面ABPE所成的二面角的余弦值;
(2)線段PD上是否存在一點N,使得直線BN與平面PCD所成角的正弦值等于![]() ?若存在,試確定點N的位置;若不存在,請說明理由.
?若存在,試確定點N的位置;若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com