
【題目】如果存在非零常數(shù)![]() ,對(duì)于函數(shù)
,對(duì)于函數(shù)![]() 定義域上的任意
定義域上的任意![]() ,都有
,都有![]() 成立,那么稱(chēng)函數(shù)為“
成立,那么稱(chēng)函數(shù)為“![]() 函數(shù)”.
函數(shù)”.
(Ⅰ)若![]() ,
,![]() ,試判斷函數(shù)
,試判斷函數(shù)![]() 和
和![]() 是否是“
是否是“![]() 函數(shù)”?若是,請(qǐng)證明:若不是,主說(shuō)明理由:
函數(shù)”?若是,請(qǐng)證明:若不是,主說(shuō)明理由:
(Ⅱ)求證:若![]() 是單調(diào)函數(shù),則它是“
是單調(diào)函數(shù),則它是“![]() 函數(shù)”;
函數(shù)”;
(Ⅲ)若函數(shù)![]() 是“
是“![]() 函數(shù)”,求實(shí)數(shù)
函數(shù)”,求實(shí)數(shù)![]() 滿(mǎn)足的條件.
滿(mǎn)足的條件.
【答案】(Ⅰ)![]() 是“
是“![]() 函數(shù)”,
函數(shù)”, ![]() 不是“
不是“![]() 函數(shù)”.理由見(jiàn)解析;(Ⅱ)證明見(jiàn)解析;(Ⅲ)
函數(shù)”.理由見(jiàn)解析;(Ⅱ)證明見(jiàn)解析;(Ⅲ)![]()
【解析】
(Ⅰ)根據(jù)定義,代入解析式解不等式,分析是否存在C使得不等式恒成立,即可判斷是否是“![]() 函數(shù)”.
函數(shù)”.
(Ⅱ)討論函數(shù)![]() 單調(diào)遞增與單調(diào)遞減兩種情況,結(jié)合函數(shù)單調(diào)的性質(zhì)即可證明
單調(diào)遞增與單調(diào)遞減兩種情況,結(jié)合函數(shù)單調(diào)的性質(zhì)即可證明![]() 是 “
是 “![]() 函數(shù)”;
函數(shù)”;
(Ⅲ)根據(jù)題意可知![]() 為單調(diào)函數(shù).代入
為單調(diào)函數(shù).代入![]() 后變形,可得關(guān)于
后變形,可得關(guān)于![]() 的一元二次不等式,結(jié)合二次函數(shù)恒成立的解法,即可求得
的一元二次不等式,結(jié)合二次函數(shù)恒成立的解法,即可求得![]() 的取值范圍.
的取值范圍.
(Ⅰ)![]() 是“
是“![]() 函數(shù)”,
函數(shù)”, ![]() 不是“
不是“![]() 函數(shù)”.理由如下:
函數(shù)”.理由如下:
若![]() 是“
是“![]() 函數(shù)”
函數(shù)”
則滿(mǎn)足![]()
即![]() ,所以
,所以![]()
解得![]() ,
,
即存在![]() 使
使![]() 是“
是“![]() 函數(shù)”
函數(shù)”
若![]() 是“
是“![]() 函數(shù)”
函數(shù)”
則滿(mǎn)足![]()
即![]() ,化簡(jiǎn)得
,化簡(jiǎn)得![]()
當(dāng)![]() 時(shí),
時(shí),![]() 不能恒成立
不能恒成立
當(dāng)![]() 時(shí),
時(shí),![]() 不能恒成立,
不能恒成立,
綜上可知,![]() 不是“
不是“![]() 函數(shù)”
函數(shù)”
(Ⅱ)證明:因?yàn)?/span>![]() 是單調(diào)函數(shù),則為單調(diào)遞增函數(shù)或單調(diào)遞減函數(shù).
是單調(diào)函數(shù),則為單調(diào)遞增函數(shù)或單調(diào)遞減函數(shù).
若![]() 是單調(diào)遞增函數(shù),則當(dāng)
是單調(diào)遞增函數(shù),則當(dāng)![]() 時(shí),都有
時(shí),都有![]() 成立,函數(shù)
成立,函數(shù)![]() 為“
為“![]() 函數(shù)”
函數(shù)”
若![]() 是單調(diào)遞減函數(shù),則當(dāng)
是單調(diào)遞減函數(shù),則當(dāng)![]() 時(shí),都有
時(shí),都有![]() 成立,函數(shù)
成立,函數(shù)![]() 為“
為“![]() 函數(shù)”
函數(shù)”
綜上可知,當(dāng)![]() 為單調(diào)函數(shù)時(shí),則它是“
為單調(diào)函數(shù)時(shí),則它是“![]() 函數(shù)”
函數(shù)”
(Ⅲ)若函數(shù)![]() 是“
是“![]() 函數(shù)”,
函數(shù)”,
由![]() ,
,
則![]()
化簡(jiǎn)可得![]() 恒成立
恒成立
由二次函數(shù)性質(zhì)可知滿(mǎn)足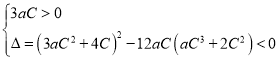
解得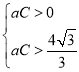
所以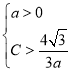 或
或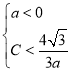
即![]() 時(shí),總存在C滿(mǎn)足函數(shù)
時(shí),總存在C滿(mǎn)足函數(shù)![]() 是“
是“![]() 函數(shù)”
函數(shù)”
所以![]() 滿(mǎn)足的條件為
滿(mǎn)足的條件為![]()


 學(xué)而優(yōu)銜接教材南京大學(xué)出版社系列答案
學(xué)而優(yōu)銜接教材南京大學(xué)出版社系列答案 小學(xué)課堂作業(yè)系列答案
小學(xué)課堂作業(yè)系列答案 金博士一點(diǎn)全通系列答案
金博士一點(diǎn)全通系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】新高考改革后,假設(shè)某命題省份只統(tǒng)一考試數(shù)學(xué)和語(yǔ)文,英語(yǔ)學(xué)科改為參加等級(jí)考試,每年考兩次,分別放在每個(gè)學(xué)年的上下學(xué)期,其余六科政治,歷史,地理,物理,化學(xué),生物則以該省的省會(huì)考成績(jī)?yōu)闇?zhǔn).考生從中選擇三科成績(jī),參加大學(xué)相關(guān)院校的錄取.
(1)若英語(yǔ)等級(jí)考試有一次為優(yōu),即可達(dá)到某“雙一流”院校的錄取要求.假設(shè)某考生參加每次英語(yǔ)等級(jí)考試事件是相互獨(dú)立的,且該生英語(yǔ)等級(jí)考試成績(jī)?yōu)閮?yōu)的概率為![]() ,求該考生直到高二下期英語(yǔ)等級(jí)考試才為優(yōu)的概率;
,求該考生直到高二下期英語(yǔ)等級(jí)考試才為優(yōu)的概率;
(2)據(jù)預(yù)測(cè),要想報(bào)考某“雙一流”院校,省會(huì)考的六科成績(jī)都在95分以上,才有可能被該校錄取.假設(shè)某考生在省會(huì)考六科的成績(jī),考到95分以上的概率都是![]() ,設(shè)該考生在省會(huì)考時(shí)考到95以上的科目數(shù)為
,設(shè)該考生在省會(huì)考時(shí)考到95以上的科目數(shù)為![]() ,求
,求![]() 的分布列及數(shù)學(xué)期望.
的分布列及數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某種汽車(chē)的購(gòu)車(chē)費(fèi)用是10萬(wàn)元,每年使用的保險(xiǎn)費(fèi)、養(yǎng)路費(fèi)、汽油費(fèi)約為![]() 萬(wàn)元,年維修費(fèi)用第一年是
萬(wàn)元,年維修費(fèi)用第一年是![]() 萬(wàn)元,第二年是
萬(wàn)元,第二年是![]() 萬(wàn)元,第三年是
萬(wàn)元,第三年是![]() 萬(wàn)元,…,以后逐年遞增
萬(wàn)元,…,以后逐年遞增![]() 萬(wàn)元汽車(chē)的購(gòu)車(chē)費(fèi)用、每年使用的保險(xiǎn)費(fèi)、養(yǎng)路費(fèi)、汽油費(fèi)、維修費(fèi)用的和平均攤到每一年的費(fèi)用叫做年平均費(fèi)用.設(shè)這種汽車(chē)使用
萬(wàn)元汽車(chē)的購(gòu)車(chē)費(fèi)用、每年使用的保險(xiǎn)費(fèi)、養(yǎng)路費(fèi)、汽油費(fèi)、維修費(fèi)用的和平均攤到每一年的費(fèi)用叫做年平均費(fèi)用.設(shè)這種汽車(chē)使用![]() 年的維修費(fèi)用的和為
年的維修費(fèi)用的和為![]() ,年平均費(fèi)用為
,年平均費(fèi)用為![]() .
.
(1)求出函數(shù)![]() ,
,![]() 的解析式;
的解析式;
(2)這種汽車(chē)使用多少年時(shí),它的年平均費(fèi)用最小?最小值是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四棱錐![]() 中,
中,![]() 平面ABCD,底面ABCD是正方形,
平面ABCD,底面ABCD是正方形,![]() ,E為PC上一點(diǎn),當(dāng)F為DC的中點(diǎn)時(shí),EF平行于平面PAD.
,E為PC上一點(diǎn),當(dāng)F為DC的中點(diǎn)時(shí),EF平行于平面PAD.
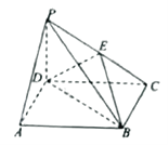
(Ⅰ)求證:![]() 平面PCB;
平面PCB;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】2015年我國(guó)將加快階梯水價(jià)推行,原則是“保基本、建機(jī)制、促節(jié)約”,其中“保基本”是指保證至少80%的居民用戶(hù)用水價(jià)格不變.為響應(yīng)國(guó)家政策,制定合理的階梯用水價(jià)格,某城市采用簡(jiǎn)單隨機(jī)抽樣的方法分別從郊區(qū)和城區(qū)抽取5戶(hù)和20戶(hù)居民的年人均用水量進(jìn)行調(diào)研,抽取的數(shù)據(jù)的莖葉圖如下(單位:噸):

(1)在郊區(qū)的這5戶(hù)居民中隨機(jī)抽取2戶(hù),求其年人均用水量都不超過(guò)30噸的概率;
(2)設(shè)該城市郊區(qū)和城區(qū)的居民戶(hù)數(shù)比為![]() ,現(xiàn)將年人均用水量不超過(guò)30噸的用戶(hù)定義為第一階梯用戶(hù),并保證這一梯次的居民用戶(hù)用水價(jià)格保持不變.試根據(jù)樣本估計(jì)總體的思想,分析此方案是否符合國(guó)家“保基本”政策.
,現(xiàn)將年人均用水量不超過(guò)30噸的用戶(hù)定義為第一階梯用戶(hù),并保證這一梯次的居民用戶(hù)用水價(jià)格保持不變.試根據(jù)樣本估計(jì)總體的思想,分析此方案是否符合國(guó)家“保基本”政策.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)函數(shù)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,對(duì)于區(qū)間
,對(duì)于區(qū)間![]() ,若
,若![]() 滿(mǎn)足
滿(mǎn)足![]() ,則稱(chēng)區(qū)間
,則稱(chēng)區(qū)間![]() 為函數(shù)
為函數(shù)![]() 的
的![]() 區(qū)間.
區(qū)間.
(1)證明:區(qū)間![]() 是函數(shù)
是函數(shù)![]() 的
的![]() 區(qū)間;
區(qū)間;
(2)若區(qū)間![]() 是函數(shù)
是函數(shù)![]() 的
的![]() 區(qū)間,求實(shí)數(shù)
區(qū)間,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)已知函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的圖象連續(xù)不斷,且在
上的圖象連續(xù)不斷,且在![]() 上僅有
上僅有![]() 個(gè)零點(diǎn),證明:區(qū)間
個(gè)零點(diǎn),證明:區(qū)間![]() 不是函數(shù)
不是函數(shù)![]() 的
的![]() 區(qū)間.
區(qū)間.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】從0、2、4中取一個(gè)數(shù)字,從1、3、5中取兩個(gè)數(shù)字,組成無(wú)重復(fù)數(shù)字的三位數(shù),則所有不同的三位數(shù)的個(gè)數(shù)是______(用數(shù)字作答)
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】學(xué)校藝術(shù)節(jié)對(duì)同一類(lèi)的![]() ,
,![]() ,
,![]() ,
,![]() 四項(xiàng)參賽作品,只評(píng)一項(xiàng)一等獎(jiǎng),在評(píng)獎(jiǎng)揭曉前,甲、乙、丙、丁四位同學(xué)對(duì)這四項(xiàng)參賽作品預(yù)測(cè)如下:
四項(xiàng)參賽作品,只評(píng)一項(xiàng)一等獎(jiǎng),在評(píng)獎(jiǎng)揭曉前,甲、乙、丙、丁四位同學(xué)對(duì)這四項(xiàng)參賽作品預(yù)測(cè)如下:
甲說(shuō):“是![]() 或
或![]() 作品獲得一等獎(jiǎng)”;
作品獲得一等獎(jiǎng)”;
乙說(shuō):“![]() 作品獲得一等獎(jiǎng)”;
作品獲得一等獎(jiǎng)”;
丙說(shuō):“![]() ,
,![]() 兩項(xiàng)作品未獲得一等獎(jiǎng)”;
兩項(xiàng)作品未獲得一等獎(jiǎng)”;
丁說(shuō):“是![]() 作品獲得一等獎(jiǎng)”.
作品獲得一等獎(jiǎng)”.
若這四位同學(xué)中只有兩位說(shuō)的話是對(duì)的,則獲得一等獎(jiǎng)的作品是__________.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com