【題目】隨著智能手機和電子閱讀器越來越普及，人們的閱讀習慣也發生了改變，手機和電子閱讀產品方便易攜帶，越來越多的人習慣通過手機或電子閱讀器閱讀.某電子書閱讀器廠商隨機調查了
人，統計了這
人每日平均通過手機或電子閱讀器閱讀的時間（單位：分鐘），由統計數據得到如下頻率分布直方圖，已知閱讀時間在
， 
， 
三組對應的人數依次成等差數列.
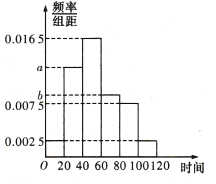
（1）求頻率分布直方圖中
， 
的值；
（2）若將日平均閱讀時間不少于
分鐘的用戶定義為“電子閱讀發燒友”，將日平均閱讀時間少于
分鐘的用戶定義為“電子閱讀潛在愛好者”，現從上述“電子閱讀發燒友”與“電子閱讀潛在愛好者”的人中按分層抽樣選出
人，再從這
人中任取
人，求恰有
人為“電子閱讀發燒友”的概率.
【答案】（1）
；（2）
【解析】試題分析：（1）由
，解得
，
又
，∴
；（2）根據分層抽樣方法可得抽取“發燒友”抽取
人，“潛在愛好者”抽取
人，利用列舉法可得這
人中任選
人的事件有
個，其中從
人中任取
人恰有
人為“電子閱讀發燒友”的事件共有
種，根據古典概型概率公式可得結果.
試題解析：（1）由
，
解得
，
又
，∴
.
（2）“電子閱讀發燒友”“電子閱讀潛在愛好者”的人數之比為： 
，所以“發燒友”抽取
人，
“潛在愛好者”抽取
人，
記事件
：從
人中任取
人恰有
人為“電子閱讀發燒友”，
設兩名“電子閱讀發燒友”的人記為： 
， 
，三名“電子閱讀潛在愛好者”的人記為： 
， 
， 
，
則這
人中任選
人有：
， 
， 
， 
， 
， 
， 
， 
， 
， 
，共
種情形，
符合題設條件的有：
， 
， 
， 
， 
， 
共有
種，
因此恰有
人為“電子閱讀發燒友”的概率為
.
科目：高中數學 來源： 題型：
【題目】[選修4一4:坐標系與參數方程]已知直線l過原點且傾斜角為
， 
，以原點O為極點，x軸的非負半軸為極軸建立極坐標系，曲線C 的極坐標方程為psin
=4cos
.
(I)寫出直線l的極坐標方程和曲線C 的直角坐標方程;
(Ⅱ)已知直線l過原點且與直線l相互垂直,若l
C=-M,l
C=N,其中M,N不與原點重合，求△OMN 面積的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學高一女生共有450人，為了了解高一女生的身高情況，隨機抽取部分高一女生測量身高，所得數據整理后列出頻率分布表如下：
組別 | 頻數 | 頻率 |
145.5～149.5 | 8 | 0.16 |
149.5～153.5 | 6 | 0.12 |
153.5～157.5 | 14 | 0.28 |
157.5～161.5 | 10 | 0.20 |
161.5～165.5 | 8 | 0.16 |
165.5～169.5 |
|
|
合計 |
|
|
（1）求出表中字母
所對應的數值；
（2）在給出的直角坐標系中畫出頻率分布直方圖；
（3）估計該校高一女生身高在149.5～165.5
范圍內有多少人？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}滿足a1＝3，a2
，且2an+1＝3an﹣an-1.
（1）求證：數列{an+1﹣an}是等比數列，并求數列{an}通項公式；
（2）求數列{nan}的前n項和為Tn，若
對任意的正整數n恒成立，求k的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現安排甲、乙、丙、丁、戊5名同學參加2022年杭州亞運會志愿者服務活動，有翻譯、導游、禮儀、司機四項工作可以安排，以下說法正確的是（ ）
A. 每人都安排一項工作的不同方法數為
B. 每項工作至少有一人參加，則不同的方法數為
C. 如果司機工作不安排，其余三項工作至少安排一人，則這5名同學全部被安排的不同方法數為
D. 每項工作至少有一人參加，甲、乙不會開車但能從事其他三項工作，丙、丁、戊都能勝任四項工作，則不同安排方案的種數是
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某大學高等數學這學期分別用
兩種不同的數學方式試驗甲、乙兩個大一新班（人數均為60人，入學數學平均分和優秀率都相同；勤奮程度和自覺性都一樣）.現隨機抽取甲、乙兩班各20名的高等數學期末考試成績，得到莖葉圖。 學校規定：成績不得低于85分的為優秀
（1）根據以上數據填寫下列的
的列聯表
甲 | 乙 | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
（2）是否有
的把握認為成績優異與教學方式有關？”(計算保留三位有效數字)
下面臨界值表僅供參考：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知定義在
上的函數
和數列
滿足下列條件：
，
，當
且
時，
且
，其中
、
均為非零常數．
（1）若是等差數列，求實數的值；
（2）令
（），若
，求數列
的通項公式；
（3）令（），若
，數列
滿足
，若數列有最大值
，最小值
，且
，求的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(2016·山東卷)已知數列{an}的前n項和Sn＝3n2＋8n，{bn}是等差數列，且an＝bn＋bn＋1.
(1)求數列{bn}的通項公式；
(2)令cn＝
，求數列{cn}的前n項和Tn.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
