
【題目】已知函數(shù)![]() ,函數(shù)g(x)=-2x+3.
,函數(shù)g(x)=-2x+3.
(1)當(dāng)a=2時(shí),求f(x)的極值;
(2)討論函數(shù)![]() 的單調(diào)性;
的單調(diào)性;
(3)若-2≤a≤-1,對任意x1,x2∈[1,2],不等式|f(x1)-f(x2)|≤t|g(x1)-g(x2)|恒成立,求實(shí)數(shù)t的最小值.
【答案】(1)f(x)極大值=f(1)=0,無極小值
(2)當(dāng)a≤0時(shí),F(x)在(0,+∞)單調(diào)遞增;當(dāng)a>0時(shí),F(x)在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減
單調(diào)遞減
(3)![]() .
.
【解析】
(1)當(dāng)a=2時(shí),利用導(dǎo)數(shù)求得函數(shù)![]() 的單調(diào)區(qū)間,進(jìn)而得到極值.
的單調(diào)區(qū)間,進(jìn)而得到極值.
(2)求得![]() ,分a≤0和a>0,兩種情況討論,即可得出函數(shù)的單調(diào)區(qū)間;
,分a≤0和a>0,兩種情況討論,即可得出函數(shù)的單調(diào)區(qū)間;
(3)把不等式轉(zhuǎn)化為f(x2)-f(x1)≤t[g(x1)-g(x2)],得到f(x2)+tg(x2)≤f(x1)+tg(x1)對任意-2≤a≤-1,1≤x1≤x2≤2恒成立,令![]() ,得到h(x)在[1,2]遞減,求得
,得到h(x)在[1,2]遞減,求得![]() 對任意a∈[-2,-1],x∈[1,2]恒成立,進(jìn)而轉(zhuǎn)化變量只需要研究
對任意a∈[-2,-1],x∈[1,2]恒成立,進(jìn)而轉(zhuǎn)化變量只需要研究![]() ,即可求得t的取值范圍.
,即可求得t的取值范圍.
(1)由題意,當(dāng)a=2時(shí),函數(shù)f(x)=lnx-x2+x,
則![]() .
.
易知f(x)在(0,1)遞增,(1,+∞)遞減,
所以函數(shù)f(x)極大值為![]() ,無極小值.
,無極小值.
(2)由函數(shù)![]() ,
,
則![]() .
.
①a≤0時(shí),![]() >0,恒成立,∴F(x)在(0,+∞)單調(diào)遞增;
>0,恒成立,∴F(x)在(0,+∞)單調(diào)遞增;
②當(dāng)a>0,由![]() >0得
>0得![]() ,
,![]() <0得
<0得![]() ,
,
所以F(x)在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減.
單調(diào)遞減.
綜上:當(dāng)a≤0時(shí),F(x)在(0,+∞)單調(diào)遞增;
當(dāng)a>0時(shí),F(x)在![]() 單調(diào)遞增,在
單調(diào)遞增,在![]() 單調(diào)遞減.
單調(diào)遞減.
(3)由題知t≥0,![]() .
.
當(dāng)-2≤a≤-1時(shí),f′(x)>0,f(x)在(0,+∞)單調(diào)遞增,不妨設(shè)1≤x1≤x2≤2,
又g(x)單調(diào)遞減,∴不等式等價(jià)于f(x2)-f(x1)≤t[g(x1)-g(x2)].
即f(x2)+tg(x2)≤f(x1)+tg(x1)對任意-2≤a≤-1,1≤x1≤x2≤2恒成立,
記![]() ,則h(x)在[1,2]遞減.
,則h(x)在[1,2]遞減.
![]() 對任意a∈[-2,-1],x∈[1,2]恒成立.
對任意a∈[-2,-1],x∈[1,2]恒成立.
令![]() .
.
則![]() 在[1,2]上恒成立,
在[1,2]上恒成立,
則![]() ,
,
而![]() 在[1,2]單調(diào)遞增,∴
在[1,2]單調(diào)遞增,∴![]() ,所以
,所以![]() .
.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知復(fù)數(shù)![]() 滿足
滿足![]() ,
,![]() 的虛部為2,
的虛部為2,
(1)求復(fù)數(shù)![]() ;
;
(2)設(shè)![]() 在復(fù)平面上對應(yīng)點(diǎn)分別為
在復(fù)平面上對應(yīng)點(diǎn)分別為![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】正方體![]() 的棱長為1,
的棱長為1,![]() 分別為
分別為![]() 的中點(diǎn).則( )
的中點(diǎn).則( )

A.直線![]() 與直線
與直線![]() 垂直B.直線
垂直B.直線![]() 與平面
與平面![]() 平行
平行
C.平面![]() 截正方體所得的截面面積為
截正方體所得的截面面積為![]() D.點(diǎn)
D.點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() 到平面
到平面![]() 的距離相等
的距離相等
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(Ⅰ)求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(Ⅱ)設(shè)![]() ,若對任意
,若對任意![]() 、
、![]() ,且
,且![]() ,都有
,都有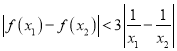 ,求實(shí)數(shù)
,求實(shí)數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)f(x)是定義域?yàn)?/span>R的偶函數(shù),且f(x+3)=f(x-1),若當(dāng)x∈[-2,0]時(shí),f(x)=2-x,記![]() ,
,![]() ,c=f(32),則a,b,c的大小關(guān)系為( )
,c=f(32),則a,b,c的大小關(guān)系為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() 位數(shù)滿足下列條件:①各個(gè)數(shù)字只能從集合
位數(shù)滿足下列條件:①各個(gè)數(shù)字只能從集合![]() 中選取;②若其中有數(shù)字4,則在4的前面不含2.將這樣的n位數(shù)的個(gè)數(shù)記為
中選取;②若其中有數(shù)字4,則在4的前面不含2.將這樣的n位數(shù)的個(gè)數(shù)記為![]()
(1)求![]() ;
;
(2)探究![]() 與
與![]() 之間的關(guān)系,求出數(shù)列
之間的關(guān)系,求出數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(3)對于每個(gè)正整數(shù)![]() ,在
,在![]() 與
與![]() 之間插入
之間插入![]() 個(gè)
個(gè)![]() 得到一個(gè)新數(shù)列
得到一個(gè)新數(shù)列![]() ,設(shè)
,設(shè)![]() 是數(shù)列
是數(shù)列![]() 的前
的前![]() 項(xiàng)和,試探究
項(xiàng)和,試探究![]() 能否成立?寫出你探究得到的結(jié)論并給出證明.
能否成立?寫出你探究得到的結(jié)論并給出證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
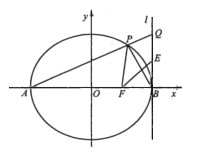
【題目】在平面直角坐標(biāo)系xOy中,已知橢圓C:![]() 的左、右頂點(diǎn)為A,B,右焦點(diǎn)為F.過點(diǎn)A且斜率為k(
的左、右頂點(diǎn)為A,B,右焦點(diǎn)為F.過點(diǎn)A且斜率為k(![]() )的直線交橢圓C于另一點(diǎn)P.
)的直線交橢圓C于另一點(diǎn)P.
(1)求橢圓C的離心率;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)設(shè)直線l:![]() ,延長AP交直線l于點(diǎn)Q,線段BQ的中點(diǎn)為E,求證:點(diǎn)B關(guān)于直線EF的對稱點(diǎn)在直線PF上.
,延長AP交直線l于點(diǎn)Q,線段BQ的中點(diǎn)為E,求證:點(diǎn)B關(guān)于直線EF的對稱點(diǎn)在直線PF上.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在長方體![]() ,中,
,中,![]() ,過
,過![]() 三點(diǎn)的平面D截去長方體的一個(gè)角后,得到如圖所示的幾何體
三點(diǎn)的平面D截去長方體的一個(gè)角后,得到如圖所示的幾何體![]() .
.
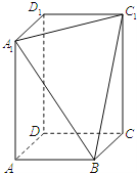
(1)求幾何體![]() 的體積;
的體積;
(2)求直線![]() 與面
與面![]() 所成角.(用反三角表示)
所成角.(用反三角表示)
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com