
【題目】已知數列{an}的前n項和為Sn , 點(n, ![]() )在直線y=
)在直線y= ![]() x+
x+ ![]() 上.
上.
(1)求數列{an}的通項公式;
(2)設bn= ![]() ,求數列{bn}的前n項和為Tn , 并求使不等式Tn>
,求數列{bn}的前n項和為Tn , 并求使不等式Tn> ![]() 對一切n∈N*都成立的最大正整數k的值.
對一切n∈N*都成立的最大正整數k的值.
【答案】
(1)解:由題意,得 ![]() =
= ![]() ,化為Sn=
,化為Sn= ![]() .
.
故當n≥2時,an=Sn﹣Sn﹣1= ![]() ﹣
﹣ ![]() =n+5,
=n+5,
當n=1時,a1=S1=6=1+5,
∴an=n+5.
(2)解:bn= ![]() =
= ![]() =
= ![]() ,
,
∴Tn= ![]() +…+
+…+ ![]()
= ![]() =
= ![]() .
.
由于Tn+1﹣Tn= ![]() =
= ![]() >0,
>0,
因此Tn單調遞增,
故(Tn)min=1.
令1 ![]() ,解得k<20,
,解得k<20,
∴kmax=19
【解析】(1)由題意,得 ![]() =
= ![]() ,化為Sn=
,化為Sn= ![]() . 利用遞推關系即可得出.(2)利用“裂項求和”可得Tn , 再利用數列的單調性、不等式的性質即可得出.
. 利用遞推關系即可得出.(2)利用“裂項求和”可得Tn , 再利用數列的單調性、不等式的性質即可得出.
【考點精析】通過靈活運用數列的前n項和和數列的通項公式,掌握數列{an}的前n項和sn與通項an的關系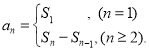 ;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式即可以解答此題.
;如果數列an的第n項與n之間的關系可以用一個公式表示,那么這個公式就叫這個數列的通項公式即可以解答此題.


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() :
: ![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)分別求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設直線![]() 交曲線
交曲線![]() 于
于![]() ,
, ![]() 兩點,交曲線
兩點,交曲線![]() 于
于![]() ,
, ![]() 兩點,求
兩點,求![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某運動員每次投籃命中的概率等于![]() .現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率:先由計算器產生0到9之間取整數值的隨機數,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三個隨機數為一組,代表三次投籃的結果.經隨機模擬產生了如下20組隨機數:
.現采用隨機模擬的方法估計該運動員三次投籃恰有兩次命中的概率:先由計算器產生0到9之間取整數值的隨機數,指定1,2,3,4表示命中,5,6,7,8,9,0,表示不命中;再以每三個隨機數為一組,代表三次投籃的結果.經隨機模擬產生了如下20組隨機數:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
據此估計,該運動員三次投籃恰有兩次命中的概率為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了提高產品的年產量,某企業擬在2013年進行技術改革,經調查測算,產品當年的產量x萬件與投入技術改革費用m萬元(m≥0)滿足x=3﹣ ![]() (k為常數).如果不搞技術改革,則該產品當年的產量只能是1萬件.已知2013年生產該產品的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元.由于市場行情較好,廠家生產均能銷售出去,廠家將每件產品的銷售價格定為每件產品生產成本的1.5倍(生產成本包括固定投入和再投入兩部分資金)
(k為常數).如果不搞技術改革,則該產品當年的產量只能是1萬件.已知2013年生產該產品的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元.由于市場行情較好,廠家生產均能銷售出去,廠家將每件產品的銷售價格定為每件產品生產成本的1.5倍(生產成本包括固定投入和再投入兩部分資金)
(1)試確定k的值,并將2013年該產品的利潤y萬元表示為技術改革費用m萬元的函數(利潤=銷售金額﹣生產成本﹣技術改革費用);
(2)該企業2013年的技術改革費用投入多少萬元時,廠家的利潤最大?并求出最大利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC是斜三角形,內角A、B、C所對的邊的長分別為a、b、c.若csinA= ![]() acosC.
acosC.
(1)求角C;
(2)若c= ![]() ,且sinC+sin(B﹣A)=5sin2A,求△ABC的面積.
,且sinC+sin(B﹣A)=5sin2A,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知{an}為等差數列,且a3=﹣6,a6=0.
(1)求{an}的通項公式.
(2)若等比數列{bn}滿足b1=8,b2=a1+a2+a3 , 求{bn}的前n項和公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是一個公差大于0的等差數列,且滿足![]() ,a2+a7=16
,a2+a7=16
(1)求數列{an}的通項公式;
(2)數列{an}和數列{bn}滿足等式![]() (n∈N*),求數列{bn}的前n項和Sn.
(n∈N*),求數列{bn}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校為倡導全體學生為特困學生捐款,舉行“一元錢,一片心,誠信用水”活動,學生在購水處每領取一瓶礦泉水,便自覺向捐款箱中至少投入一元錢.現統計了連續5天的售出和收益情況,如表:
售出水量x(單位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(單位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y關于x的線性回歸方程;
(2)預測售出8箱水的收益是多少元?
附:回歸直線的斜率和截距的最小二乘法估計公式分別為: ![]() =
= 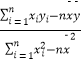 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,
,
參考數據:7×165+6×142+6×148+5×125+6×150=4420.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com