
【題目】設(shè)函數(shù)f(x)=x ![]() +bx,曲線y=f(x)在點(diǎn) (2,f(2))處的切線方程為y=(e-1)x+4,
+bx,曲線y=f(x)在點(diǎn) (2,f(2))處的切線方程為y=(e-1)x+4,
(1)求a,b的值;
(2)求f(x)的單調(diào)區(qū)間。
【答案】
(1)
解: ![]()
∴ ![]()
∵曲線 ![]() 在點(diǎn)
在點(diǎn) ![]() 處的切線方程為
處的切線方程為 ![]()
∴ ![]() ,
, ![]()
即 ![]() ①
①
![]() ②
②
由①②解得: ![]() ,
, ![]()
(2)
解:∵a=2,b=e;
∴f(x)=xe2﹣x+ex,
∴f′(x)=e2﹣x﹣xe2﹣x+e=(1﹣x)e2﹣x+e,
f″(x)=﹣e2﹣x﹣(1﹣x)e2﹣x=(x﹣2)e2﹣x,
由f″(x)>0得x>2,由f″(x)<0得x<2,
即當(dāng)x=2時(shí),f′(x)取得極小值f′(2)=(1﹣2)e2﹣2+e=e﹣1>0,
∴f′(x)>0恒成立,
即函數(shù)f(x)是增函數(shù),
即f(x)的單調(diào)區(qū)間是(﹣∞,+∞).
【解析】(1)求函數(shù)的導(dǎo)數(shù),根據(jù)導(dǎo)數(shù)的幾何意義求出函數(shù)的切線斜率以及f(2),建立方程組關(guān)系即可求a,b的值;(2)求函數(shù)的導(dǎo)數(shù),利用函數(shù)單調(diào)性和導(dǎo)數(shù)之間的關(guān)系即可求f(x)的單調(diào)區(qū)間.
【考點(diǎn)精析】通過(guò)靈活運(yùn)用利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性,掌握一般的,函數(shù)的單調(diào)性與其導(dǎo)數(shù)的正負(fù)有如下關(guān)系: 在某個(gè)區(qū)間![]() 內(nèi),(1)如果
內(nèi),(1)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個(gè)區(qū)間單調(diào)遞增;(2)如果
在這個(gè)區(qū)間單調(diào)遞增;(2)如果![]() ,那么函數(shù)
,那么函數(shù)![]() 在這個(gè)區(qū)間單調(diào)遞減即可以解答此題.
在這個(gè)區(qū)間單調(diào)遞減即可以解答此題.


 狀元坊全程突破導(dǎo)練測(cè)系列答案
狀元坊全程突破導(dǎo)練測(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖為一個(gè)纜車(chē)示意圖,該纜車(chē)半徑為4.8m,圓上最低點(diǎn)與地面距離為0.8m,60秒轉(zhuǎn)動(dòng)一圈,圖中OA與地面垂直,以OA為始邊,逆時(shí)針轉(zhuǎn)動(dòng)θ角到OB,設(shè)B點(diǎn)與地面距離是h.
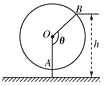
(1)求h與θ間的函數(shù)關(guān)系式;
(2)設(shè)從OA開(kāi)始轉(zhuǎn)動(dòng),經(jīng)過(guò)t秒后到達(dá)OB,求h與t之間的函數(shù)關(guān)系式,并求纜車(chē)到達(dá)最高點(diǎn)時(shí)用的最少時(shí)間是多少?
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() 是數(shù)列
是數(shù)列![]() 的前n項(xiàng)和,并且
的前n項(xiàng)和,并且![]() ,對(duì)任意正整數(shù)n,
,對(duì)任意正整數(shù)n, ![]() ;設(shè)
;設(shè)
![]() .
.
(Ⅰ) 證明:數(shù)列![]() 是等比數(shù)列,并求
是等比數(shù)列,并求![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅱ) 設(shè)![]() ,求證: 數(shù)列
,求證: 數(shù)列![]() 不可能為等比數(shù)列。
不可能為等比數(shù)列。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】判斷下列兩圓的位置關(guān)系.
(1)C1:x2+y2-2x-3=0,C2:x2+y2-4x+2y+3=0;___________
(2)C1:x2+y2-2y=0,C2:x2+y2-2![]() x-6=0;___________
x-6=0;___________
(3)C1:x2+y2-4x-6y+9=0,C2:x2+y2+12x+6y-19=0;___________
(4)C1:x2+y2+2x-2y-2=0,C2:x2+y2-4x-6y-3=0.___________
(5)x2+y2=9和x2+y2-8x+6y+9=0 ________________
(6)圓C1:x2+y2-2x-6y-6=0與圓C2:x2+y2-4x+2y+4=0______
(7)圓x2+y2+6x-7=0和圓x2+y2+6y-27=0 ____________
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某地政府調(diào)查了工薪階層![]() 人的月工資收人,并根據(jù)調(diào)查結(jié)果畫(huà)出如圖所示的頻率分布直方圖,其中工資收人分組區(qū)間是
人的月工資收人,并根據(jù)調(diào)查結(jié)果畫(huà)出如圖所示的頻率分布直方圖,其中工資收人分組區(qū)間是![]() .(單位:百元)
.(單位:百元)

(1)為了了解工薪階層對(duì)工資收人的滿(mǎn)意程度,要用分層抽樣的方法從調(diào)查的![]() 人中抽取
人中抽取![]() 人做電話詢(xún)問(wèn),求月工資收人在
人做電話詢(xún)問(wèn),求月工資收人在![]() 內(nèi)應(yīng)抽取的人數(shù);
內(nèi)應(yīng)抽取的人數(shù);
(2)根據(jù)頻率分布直方圖估計(jì)這![]() 人的平均月工資為多少元.
人的平均月工資為多少元.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】設(shè)數(shù)列A: ![]() ,
, ![]() ,…
,… ![]() (N≥2)。如果對(duì)小于n(2≤n≤N)的每個(gè)正整數(shù)k都有
(N≥2)。如果對(duì)小于n(2≤n≤N)的每個(gè)正整數(shù)k都有 ![]() <
< ![]() ,則稱(chēng)n是數(shù)列A的一個(gè)“G時(shí)刻”。記“G(A)是數(shù)列A 的所有“G時(shí)刻”組成的集合。
,則稱(chēng)n是數(shù)列A的一個(gè)“G時(shí)刻”。記“G(A)是數(shù)列A 的所有“G時(shí)刻”組成的集合。
(1)對(duì)數(shù)列A:-2,2,-1,1,3,寫(xiě)出G(A)的所有元素;
(2)證明:若數(shù)列A中存在 ![]() 使得
使得 ![]() >
> ![]() ,則G(A)
,則G(A) ![]()
![]() ;
;
(3)證明:若數(shù)列A滿(mǎn)足 ![]() -
- ![]() ≤1(n=2,3, …,N),則GA.的元素個(gè)數(shù)不小于
≤1(n=2,3, …,N),則GA.的元素個(gè)數(shù)不小于 ![]() -
- ![]() 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知A、B是單位圓O上的兩點(diǎn)(O為圓心),∠AOB=120°,點(diǎn)C是線段AB上不與A、B重合的動(dòng)點(diǎn).MN是圓O的一條直徑,則![]() 的取值范圍是( )
的取值范圍是( )
A. [![]() ,0) B. [
,0) B. [![]() ,0] C. [
,0] C. [![]() ,1) D. [
,1) D. [![]() ,1]
,1]
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某化工廠生產(chǎn)甲、乙兩種混合肥料,需要A,B,C三種主要原料,生產(chǎn)1扯皮甲種肥料和生產(chǎn)1車(chē)皮乙種肥料所需三種原料的噸數(shù)如表所示:
配料 原料 | A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
現(xiàn)有A種原料200噸,B種原料360噸,C種原料300噸,在此基礎(chǔ)上生產(chǎn)甲、乙兩種肥料.已知生產(chǎn)1車(chē)皮甲種肥料,產(chǎn)生的利潤(rùn)為2萬(wàn)元;生產(chǎn)1車(chē)品乙種肥料,產(chǎn)生的利潤(rùn)為3萬(wàn)元、分別用x,y表示計(jì)劃生產(chǎn)甲、乙兩種肥料的車(chē)皮數(shù).
(1)用x,y列出滿(mǎn)足生產(chǎn)條件的數(shù)學(xué)關(guān)系式,并畫(huà)出相應(yīng)的平面區(qū)域;
(2)問(wèn)分別生產(chǎn)甲、乙兩種肥料,求出此最大利潤(rùn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 與拋物線
與拋物線![]() 相交于
相交于![]() 、
、![]() 兩點(diǎn).
兩點(diǎn).
(1)求證:“如果直線![]() 過(guò)點(diǎn)
過(guò)點(diǎn)![]() ,那么
,那么![]() ”是真命題;
”是真命題;
(2)寫(xiě)出(1)中命題的逆命題,判斷它是真命題還是假命題,并說(shuō)明理由.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com