
【題目】已知函數(shù)![]() .
.
(Ⅰ)求函數(shù)![]() 的單調區(qū)間;
的單調區(qū)間;
(Ⅱ)若函數(shù)![]() 上是減函數(shù),求實數(shù)a的最小值;
上是減函數(shù),求實數(shù)a的最小值;
(Ⅲ)若![]() ,
,![]() ,使
,使![]() 成立,求實數(shù)a的取值范圍.
成立,求實數(shù)a的取值范圍.
【答案】(1) 增區(qū)間是![]() 減區(qū)間是
減區(qū)間是![]() (2)
(2)![]() (3)
(3)![]()
【解析】試題分析:(1)先求導數(shù),再求導函數(shù)零點,根據(jù)零點分類討論導函數(shù)符號,確定單調區(qū)間(2)即等價于導函數(shù)![]() 上恒非正,利用變量分離,轉化為對應函數(shù)最值:
上恒非正,利用變量分離,轉化為對應函數(shù)最值:![]() 最大值,再利用導數(shù)研究函數(shù)
最大值,再利用導數(shù)研究函數(shù)![]() 最大值,即得實數(shù)a的取值范圍,進而有最小值(3)等價于
最大值,即得實數(shù)a的取值范圍,進而有最小值(3)等價于![]() ,由前兩題不難得到
,由前兩題不難得到![]() ,
,![]() ,代入即得實數(shù)a的取值范圍.
,代入即得實數(shù)a的取值范圍.
試題解析:解:由已知函數(shù)![]() 的定義域均為
的定義域均為![]() ,且
,且![]() .
.
(Ⅰ)函數(shù) 當
當![]() 時,
時,![]() .所以函數(shù)
.所以函數(shù)![]() 的單調增區(qū)間是
的單調增區(qū)間是![]() 當
當![]() 且
且![]() 時,
時, ![]() .所以函數(shù)
.所以函數(shù)![]() 的單調減區(qū)間是
的單調減區(qū)間是![]()
(Ⅱ)∵![]() 在
在![]() 上單調遞減,∴
上單調遞減,∴ ![]() 恒成立,即
恒成立,即![]() 恒成立,設
恒成立,設![]() ,∵
,∵![]() ,∴當
,∴當![]() 時,
時,![]() ∴
∴![]()
Ⅱ)因f(x)在![]() 上為減函數(shù),故
上為減函數(shù),故![]() 在
在![]() 上恒成立. 所以當
上恒成立. 所以當![]() 時
時![]() 又
又![]()
![]() , 故當
, 故當![]() ,即
,即![]() 時,
時,![]() . 所以
. 所以![]() 于是
于是![]() ,故a的最小值為
,故a的最小值為![]() .
.
(Ⅲ)由已知得“當![]() 時,有
時,有![]() ”.由(Ⅱ),當
”.由(Ⅱ),當![]() 時,
時, ![]() , 由(Ⅰ),當
, 由(Ⅰ),當![]() 時,有
時,有![]() 所以有
所以有![]() 故
故![]()


科目:高中數(shù)學 來源: 題型:
【題目】已知向量m=(cosx,-1),n=![]() ,函數(shù)f(x)=(m+n)·m.
,函數(shù)f(x)=(m+n)·m.
(1)求函數(shù)f(x)的最小正周期;
(2)已知a,b,c分別為△ABC內角A,B,C的對邊,A為銳角,a=1,c=![]() ,且f(A)恰是函數(shù)f(x)在
,且f(A)恰是函數(shù)f(x)在![]() 上的最大值,求A,b和△ABC的面積.
上的最大值,求A,b和△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在公差不為零的等差數(shù)列{an}中,已知a1=1,且a1,a2,a5依次成等比數(shù)列.數(shù)列{bn}滿足bn+1=2bn-1,且b1=3.
(1)求{an},{bn}的通項公式;
(2)設數(shù)列![]() 的前n項和為Sn,試比較Sn與1-
的前n項和為Sn,試比較Sn與1-![]() 的大小.
的大小.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某市為了制定合理的節(jié)電方案,供電局對居民用電情況進行了調查,通過抽樣,獲得了某年200戶居民每戶的月均用電量(單位:度),將數(shù)據(jù)按照![]() ,
,![]() 分成9組,制成了如圖所示的頻率直方圖.
分成9組,制成了如圖所示的頻率直方圖.
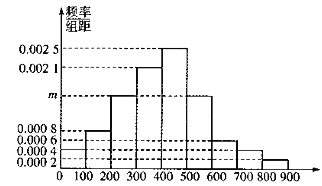
(1)求直方圖中![]() 的值并估計居民月均用電量的中位數(shù);
的值并估計居民月均用電量的中位數(shù);
(2)從樣本里月均用電量不低于700度的用戶中隨機抽取4戶,用![]() 表示月均用電量不低于800度的用戶數(shù),求隨機變量
表示月均用電量不低于800度的用戶數(shù),求隨機變量![]() 的分布列及數(shù)學期望.
的分布列及數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】甲、乙兩支排球隊進行比賽,約定先勝3局者獲得比賽的勝利,比賽隨即結束.除第五局甲隊獲勝的概率是![]() 外,其余每局比賽甲隊獲勝的概率都是
外,其余每局比賽甲隊獲勝的概率都是![]() .假設各局比賽結果相互獨立.
.假設各局比賽結果相互獨立.
(1)分別求甲隊以3:0,3:1,3:2獲勝的概率;
(2)若比賽結果為3:0或3:1,則勝利方得3分、對方得0分;若比賽結果為3:2,則勝利方得2分、對方得1分.求甲隊得分X的分布列及數(shù)學期望.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知二次函數(shù)![]() 在
在![]() 處取得極值,且在
處取得極值,且在![]() 點處的切線與直線
點處的切線與直線![]() 平行.
平行.
(1)求![]() 的解析式;
的解析式;
(2)求函數(shù)![]() 的單調遞增區(qū)間及極值。
的單調遞增區(qū)間及極值。
(3)求函數(shù)![]() 在
在![]() 的最值。
的最值。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知二次函數(shù)![]() 在
在![]() 處取得極值,且在
處取得極值,且在![]() 點處的切線與直線
點處的切線與直線![]() 平行.
平行.
(1)求![]() 的解析式;
的解析式;
(2)求函數(shù)![]() 的單調遞增區(qū)間及極值。
的單調遞增區(qū)間及極值。
(3)求函數(shù)![]() 在
在![]() 的最值。
的最值。
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com