
���}Ŀ���x��4-4������(bi��o)ϵ�c����(sh��)����
��ֱ֪��(xi��n)![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�![]() ��
��![]() �酢��(sh��)������ԭ�c(di��n)
�酢��(sh��)������ԭ�c(di��n)![]() ��O�c(di��n)��
��O�c(di��n)�� ![]() �S�������S��O�S�������O����(bi��o)ϵ������(xi��n)
�S�������S��O�S�������O����(bi��o)ϵ������(xi��n)![]() �ĘO����(bi��o)����
�ĘO����(bi��o)����![]() .
.
��1����ֱ��(xi��n)![]() ����ͨ���̼�����(xi��n)
����ͨ���̼�����(xi��n)![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
��2���O(sh��)����(xi��n)![]() �c
�c![]() �S�ăɂ�(g��)���c(di��n)�քe��
�S�ăɂ�(g��)���c(di��n)�քe��![]() ���c
���c![]() �S�����S�Ľ��c(di��n)��
�S�����S�Ľ��c(di��n)��![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() ��
��![]() �ֳɵăɲ��ֵ���e��.
�ֳɵăɲ��ֵ���e��.
���𰸡���1��![]() ��
�� ![]() ��2��
��2��![]()
����������1���ڣ�1����(w��n)��ֱ����������(bi��o)�����Ĺ�ʽ��ֱ��(xi��n)l����ͨ���̺�����(xi��n)C��ֱ������(bi��o)����. (2)�ڣ�2����(w��n)���ȷքe��![]() �ɲ��ֵ���e��.
�ɲ��ֵ���e��.
ԇ�}������
��1��![]() ��
�� ![]() ����ȥ����(sh��)
����ȥ����(sh��)![]() ����
����![]() ��
��
����ֱ��(xi��n)![]() ����ͨ���̞�
����ͨ���̞�![]() .
.
��![]() ��׃�Ξ�
��׃�Ξ�![]() ��
��
����![]()
![]() ��
��
�������(xi��n)![]() ��ֱ������(bi��o)���̞�
��ֱ������(bi��o)���̞�![]() .
.
��2���O(sh��)ֱ��(xi��n)![]() �c
�c![]() �S�Ľ��c(di��n)��
�S�Ľ��c(di��n)��![]() ���ڷ���
���ڷ���![]() �У�
�У�
��![]() ��
��![]() ������
������![]() ,
,
���ɣ�1����֪![]() ��
��
����ֱ��(xi��n)![]() ��
�� ![]() ��
��![]() ��
�� ![]() ��
��
�O(sh��)ֱ��(xi��n)![]() �cֱ��(xi��n)
�cֱ��(xi��n)![]() �����c(di��n)
�����c(di��n)![]() ��(li��n)�����̽M
��(li��n)�����̽M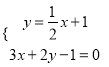
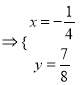 ��
��
����?x��n)�ֱ��(xi��n)���c(di��n)��![]() ��
��
����![]() ��
��
![]() ��
��
�Ķ���߅��![]() ����e
����e![]() ��
��
����![]() .
.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
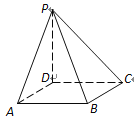
���}Ŀ���������FP�CABCD�У�����ABCD��߅�L(zh��ng)��6�������Σ�PDƽ��ABCD��PD=8��
(1) ��PB�cƽ��ABCD���ɽǵĴ�С��
(2) ����ֱ��(xi��n)PB�cDC���ɽǵĴ�С��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���O(sh��)����(sh��)![]() ��
�� ![]() ��
��
��1����![]() �Ć��{(di��o)�^(q��)�g�͘Oֵ��
�Ć��{(di��o)�^(q��)�g�͘Oֵ��
��2���C������![]() �������c(di��n)���t
�������c(di��n)���t![]() �څ^(q��)�g
�څ^(q��)�g![]() �σH��һ��(g��)���c(di��n)��
�σH��һ��(g��)���c(di��n)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij������˾����һ�����a(ch��n)Ʒ��A���\(y��n)��B�أ��F(xi��n)����܇(ch��)����܇(ch��)���w�C(j��)���N�\(y��n)ݔ���߿ɹ��x���@���N���ߵ���Ҫ������(sh��)��(j��)���£�
�\(y��n)ݔ���� | ;���ٶȣ� | ;���M(f��i)�ã�Ԫ/ | �bж�r(sh��)�g�� | �bж�M(f��i)�ã�Ԫ/ |
��܇(ch��) | 50 | 80 | 2 | 200 |
��܇(ch��) | 100 | 40 | 3 | 400 |
�w�C(j��) | 200 | 200 | 3 | 800 |
���@�����a(ch��n)Ʒ���\(y��n)ݔ�^(gu��)���еēp�Ğ�300Ԫ/![]() ����(w��n)�����ķN�\(y��n)ݔ��ʽ���^�ã����\(y��n)ݔ�^(gu��)���е��M(f��i)���c�p��֮����С.
����(w��n)�����ķN�\(y��n)ݔ��ʽ���^�ã����\(y��n)ݔ�^(gu��)���е��M(f��i)���c�p��֮����С.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У��E�A
���E�A![]() ��
�� ![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() ���ɽ��c(di��n)�c���S��һ��(g��)��c(di��n)��(g��u)�ɵ���ֱ�������Σ����c(di��n)
���ɽ��c(di��n)�c���S��һ��(g��)��c(di��n)��(g��u)�ɵ���ֱ�������Σ����c(di��n) �ڙE�A
�ڙE�A![]() ��.
��.
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2����D��ʾ���^(gu��)�E�A�����c(di��n)��ֱ��(xi��n)![]() ��б�ʴ����Ҳ���0�����E�A
��б�ʴ����Ҳ���0�����E�A![]() ��
��![]() ���c(di��n)���^(gu��)�ҽ��c(di��n)��ֱ��(xi��n)
���c(di��n)���^(gu��)�ҽ��c(di��n)��ֱ��(xi��n)![]() ���E�A
���E�A![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() ��
��![]() �S���c(di��n)
�S���c(di��n)![]() ����(d��ng)�c(di��n)
����(d��ng)�c(di��n)![]() ������
������![]() ���ڙE�A���\(y��n)��(d��ng).
���ڙE�A���\(y��n)��(d��ng).
���C���� ![]() �鳣��(sh��)��
�鳣��(sh��)��
�ڮ�(d��ng)![]() �r(sh��)�����������Y(ji��)Փ��
�r(sh��)�����������Y(ji��)Փ��![]() ��e��ȡֵ����.
��e��ȡֵ����.

�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���������к���(sh��)�Ĵ��D����(xi��)������(sh��)�Ć��{(di��o)�^(q��)�g��ֵ��
��1��![]() �� ��2��
�� ��2��![]() ����3��
����3��![]() ��
��
��4��![]() ����5��
����5��![]() ����6��
����6��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��һ�����С�Α��Ҏ(gu��)�t���£�ÿ݆�Α���������Σ�ÿ�Γ���Ҫô���F(xi��n)һ������(l��)��Ҫô�����F(xi��n)����(l��)��ÿ݆�Α�������κ��F(xi��n)һ������(l��)�@��10�֣����F(xi��n)�ɴ�����(l��)�@��20�֣����F(xi��n)��������(l��)�@��100�֣��](m��i)�г��F(xi��n)����(l��)�t�۳�200�֣����@�ã�200�֣����O(sh��)ÿ�Γ��ij��F(xi��n)����(l��)�ĸ��ʞ�![]() ���Ҹ��Γ����Ƿ���F(xi��n)����(l��)���(d��)����
���Ҹ��Γ����Ƿ���F(xi��n)����(l��)���(d��)����
��1������݆�Α�������һ݆���F(xi��n)����(l��)�ĸ����Ƕ��٣�
��2���O(sh��)ÿ݆�Α�@�õķ�?j��n)?sh��)��X����X�ķֲ��м���(sh��)�W(xu��)������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
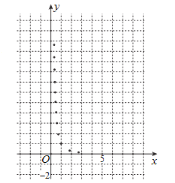
���}Ŀ��ij�W(xu��)�����˜y(c��)ԇú�����ˮ��ι�(ji��)ʡú��Ć�(w��n)�}�O(sh��)Ӌ(j��)��һ��(g��)��(sh��)�(y��n)�����@����ú���_(k��i)�P(gu��n)���o���D(zhu��n)�Ļ��Ȕ�(sh��)![]() �c���_(k��i)һ��ˮ���Õr(sh��)�g
�c���_(k��i)һ��ˮ���Õr(sh��)�g![]() ��һ�M��(sh��)��(j��)��������һ���Ĕ�(sh��)��(j��)̎��(���±�)���õ���ɢ�c(di��n)�D(���D)��
��һ�M��(sh��)��(j��)��������һ���Ĕ�(sh��)��(j��)̎��(���±�)���õ���ɢ�c(di��n)�D(���D)��
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
����![]() ��
��
��1������(j��)ɢ�c(di��n)�D�Д࣬![]() �c
�c![]() ��һ��(g��)���m������ˮ�r(sh��)�g
��һ��(g��)���m������ˮ�r(sh��)�g![]() �P(gu��n)���_(k��i)�P(gu��n)���o���D(zhu��n)�Ļ��Ȕ�(sh��)
�P(gu��n)���_(k��i)�P(gu��n)���o���D(zhu��n)�Ļ��Ȕ�(sh��)![]() �Ļؚw�����(l��i)��?(�����f(shu��)������)
�Ļؚw�����(l��i)��?(�����f(shu��)������)
��2������(j��)�Д�Y(ji��)���ͱ��Д�(sh��)��(j��)������![]() �P(gu��n)
�P(gu��n)![]() �Ļؚw���̣�
�Ļؚw���̣�
��3�������D(zhu��n)�Ļ��Ȕ�(sh��)![]() �c��λ�r(sh��)�g��(n��i)ú��ݔ����
�c��λ�r(sh��)�g��(n��i)ú��ݔ����![]() �����ȣ���ô
�����ȣ���ô![]() ����ٕr(sh��)�����_(k��i)һ��ˮ��ʡú�⣿
����ٕr(sh��)�����_(k��i)һ��ˮ��ʡú�⣿
������(du��)��һ�M��(sh��)��(j��)![]() ����ؚwֱ��(xi��n)
����ؚwֱ��(xi��n)![]() ��б�ʺͽؾ����С���˹�Ӌ(j��)�քe��
��б�ʺͽؾ����С���˹�Ӌ(j��)�քe��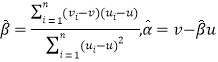 ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��![]() .�����(sh��)��
.�����(sh��)��![]() �M(m��n)��
�M(m��n)��![]() ��
�� ![]() ������
������![]() ���t�Q(ch��ng)
���t�Q(ch��ng)![]() ��
��![]() �ġ���锵(sh��)�С�.
�ġ���锵(sh��)�С�.
����(xi��)����(sh��)��![]() �ġ���锵(sh��)�С�
�ġ���锵(sh��)�С�![]() ��
��
������![]() �ġ���锵(sh��)�С���
�ġ���锵(sh��)�С���![]() .ԇ�C����
.ԇ�C���� ![]() �ɵȲ(sh��)��.
�ɵȲ(sh��)��.
������![]() ��ż��(sh��)����
��ż��(sh��)����![]() �ġ���锵(sh��)�С���
�ġ���锵(sh��)�С���![]() ���C����
���C���� ![]() .
.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com