
【題目】如圖,邊長為![]() 的正方形
的正方形![]() 和高為
和高為![]() 的等腰梯形
的等腰梯形![]() 所在的平面互相垂直,
所在的平面互相垂直,![]() ,
,![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,點
,點![]() 為線段
為線段![]() 上任意一點.
上任意一點.

(Ⅰ)求證:![]() 平面
平面![]() ;
;
(Ⅱ)求![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)是否存在點![]() 使平面
使平面![]() 與平面
與平面![]() 垂直,若存在,求出
垂直,若存在,求出![]() 的值,若不存在,說明理由.
的值,若不存在,說明理由.
【答案】(Ⅰ)詳見解析(Ⅱ)![]() (Ⅲ)存在,且此時
(Ⅲ)存在,且此時![]() 的值為
的值為![]()
【解析】
(Ⅰ)證明EF∥BD,OF∥ED.推出OF∥平面ADE;
(Ⅱ)取EF中點M,連結MO,得到MO⊥BD.證明MO⊥平面ABCD,建立空間直角坐標系O﹣xyz,求出平面ADE的法向量利用空間向量的數量積求解直線BF與平面ADE所成角;
(Ⅲ)設![]() ,求出平面BCH的法向量,通過平面BCH與平面ADE垂直,則
,求出平面BCH的法向量,通過平面BCH與平面ADE垂直,則![]() ,轉化求解即可.
,轉化求解即可.
證明:(Ⅰ)因為正方形![]() 中,
中,![]() 與
與![]() 交于點
交于點![]() ,
,
所以![]() .
.
因為![]() ,
,![]()
![]()
所以![]()
![]() 且
且![]()
所以![]() 為平行四邊形.
為平行四邊形.
所以![]()
![]() .
.
又因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
解:(Ⅱ)取![]() 中點
中點![]() ,連結
,連結![]() ,因為梯形
,因為梯形![]() 為等腰梯形,所以
為等腰梯形,所以![]() .
.
又因為平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因為![]() ,
,
所以![]() 兩兩垂直.
兩兩垂直.
如圖,建立空間直角坐標系![]() ,
,
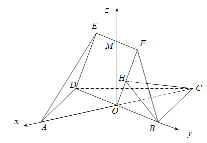
則![]()
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
則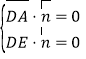 ,即
,即 ,
,
令![]() ,則
,則![]() ,所以
,所以![]() .
.
設直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,
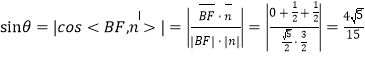 ,
,
所以直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.
(Ⅲ)設![]() ,
,
則![]() ,
,![]() ,
,![]()
設平面![]() 的法向量為
的法向量為![]() ,
,
則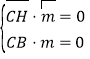 ,即
,即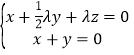 ,
,
令![]() ,則
,則![]() ,
,![]() .
.
所以![]() .
.
若平面![]() 與平面
與平面![]() 垂直,則
垂直,則![]() .
.
由![]() ,得
,得![]() .
.
所以線段OF上存在點![]() 使平面
使平面![]() 與平面
與平面![]() 垂直,
垂直,
![]() 的值為
的值為![]() .
.


科目:高中數學 來源: 題型:
【題目】某單位為了響應疫情期間有序復工復產的號召,組織從疫區回來的甲、乙、丙、丁4名員工進行核酸檢測,現采用抽簽法決定檢測順序,在“員工甲不是第一個檢測,員工乙不是最后一個檢測”的條件下,員工丙第一個檢測的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列選項中,說法正確的是( )
A.命題“![]() ,
,![]() ”的否定為“
”的否定為“![]() ,
,![]() ”;
”;
B.命題“在![]() 中,
中,![]() ,則
,則![]() ”的逆否命題為真命題;
”的逆否命題為真命題;
C.已知![]() 、m是兩條不同的直線,
、m是兩條不同的直線,![]() 是個平面,若
是個平面,若![]() ,則
,則![]() ;
;
D.已知定義在R上的函數![]() ,則“
,則“![]() 為奇函數”是“
為奇函數”是“![]() ”的充分必要條件.
”的充分必要條件.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為迎接![]() 年北京冬季奧運會,普及冬奧知識,某校開展了“冰雪答題王”冬奧知識競賽活動.現從參加冬奧知識競賽活動的學生中隨機抽取了
年北京冬季奧運會,普及冬奧知識,某校開展了“冰雪答題王”冬奧知識競賽活動.現從參加冬奧知識競賽活動的學生中隨機抽取了![]() 名學生,將他們的比賽成績(滿分為
名學生,將他們的比賽成績(滿分為![]() 分)分為
分)分為![]() 組:
組:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如圖所示的頻率分布直方圖.
,得到如圖所示的頻率分布直方圖.
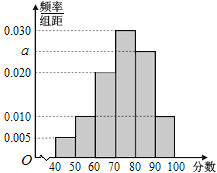
(1)求![]() 的值;
的值;
(2)記![]() 表示事件“從參加冬奧知識競賽活動的學生中隨機抽取一名學生,該學生的比賽成績不低于
表示事件“從參加冬奧知識競賽活動的學生中隨機抽取一名學生,該學生的比賽成績不低于![]() 分”,估計
分”,估計![]() 的概率;
的概率;
(3)在抽取的![]() 名學生中,規定:比賽成績不低于
名學生中,規定:比賽成績不低于![]() 分為“優秀”,比賽成績低于
分為“優秀”,比賽成績低于![]() 分為“非優秀”.請將下面的
分為“非優秀”.請將下面的![]() 列聯表補充完整,并判斷是否有
列聯表補充完整,并判斷是否有![]() 的把握認為“比賽成績是否優秀與性別有關”?
的把握認為“比賽成績是否優秀與性別有關”?
優秀 | 非優秀 | 合計 | |
男生 |
| ||
女生 |
| ||
合計 |
|
參考公式及數據: ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在極坐標系![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,弧
,弧![]() ,
,![]() 所在圓的圓心分別是
所在圓的圓心分別是![]() ,
,![]() ,曲線
,曲線![]() 是弧
是弧![]() ,曲線
,曲線![]() 是線段
是線段![]() ,曲線
,曲線![]() 是線段
是線段![]() ,曲線
,曲線![]() 是弧
是弧![]() .
.
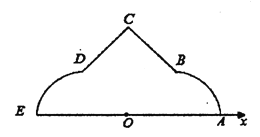
(1)分別寫出![]() ,
,![]() ,
,![]() ,
,![]() 的極坐標方程;
的極坐標方程;
(2)曲線![]() 由
由![]() ,
,![]() ,
,![]() ,
,![]() 構成,若點
構成,若點![]() ,(
,(![]() ),在
),在![]() 上,則當
上,則當![]() 時,求點
時,求點![]() 的極坐標.
的極坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列命題,其中正確的命題有( )
A.設具有相關關系的兩個變量x,y的相關系數為r,則![]() 越接近于0,x,y之間的線性相關程度越高
越接近于0,x,y之間的線性相關程度越高
B.隨機變量![]() ,若
,若![]() ,則
,則![]()
C.公共汽車上有10位乘客,沿途5個車站,乘客下車的可能方式有![]() 種
種
D.回歸方程為![]() 中,變量y與x具有正的線性相關關系,變量x增加1個單位時,y平均增加0.85個單位
中,變量y與x具有正的線性相關關系,變量x增加1個單位時,y平均增加0.85個單位
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知甲、乙兩名工人在同樣條件下每天各生產100件產品,且每生產1件正品可獲利20元,生產1件次品損失30元,甲、乙兩名工人100天中出現次品件數的情況如表所示.
甲每天生產的次品數/件 | 0 | 1 | 2 | 3 | 4 |
對應的天數/天 | 40 | 20 | 20 | 10 | 10 |
乙每天生產的次品數/件 | 0 | 1 | 2 | 3 |
對應的天數/天 | 30 | 25 | 25 | 20 |
(1)將甲每天生產的次品數記為![]() (單位:件),日利潤記為
(單位:件),日利潤記為![]() (單位:元),寫出
(單位:元),寫出![]() 與
與![]() 的函數關系式;
的函數關系式;
(2)按這100天統計的數據,分別求甲、乙兩名工人的平均日利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如果三個常用對數![]() 中,任意兩個的對數尾數之和大于第三個對數尾數,則稱這三個正數
中,任意兩個的對數尾數之和大于第三個對數尾數,則稱這三個正數![]() 可以構成一個“對數三角形”.現從集合 M={7,8,9,10,11,12,13,14} 中選擇三個互異整數作成對數三角形,則不同的選擇方案有( )種.
可以構成一個“對數三角形”.現從集合 M={7,8,9,10,11,12,13,14} 中選擇三個互異整數作成對數三角形,則不同的選擇方案有( )種.
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com