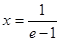已知函數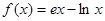 ,
,
(1)求函數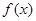 的單調區間;
的單調區間;
(2)在區間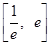 內存在
內存在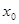 ,使不等式
,使不等式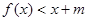 成立,求
成立,求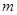 的取值范圍.
的取值范圍.
(1)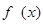 的單調遞增區間是
的單調遞增區間是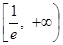 ,
, 的單調遞減區間是
的單調遞減區間是 .
.
(2) 的取值范圍是
的取值范圍是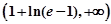 .
.
解析試題分析:(1)首先確定函數的定義域.求導數: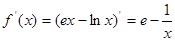 ,根據當
,根據當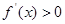 時,
時,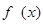 為單調遞增函數;
為單調遞增函數;
當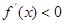 時,
時,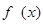 為單調遞減函數,得到函數的單調區間.
為單調遞減函數,得到函數的單調區間.
(2)構造函數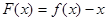 ,即
,即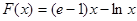 ,將問題轉化成:在區間
,將問題轉化成:在區間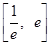 內,
內,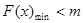 ,利用導數求函數的極值、最小值,得到
,利用導數求函數的極值、最小值,得到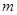 的取值范圍是
的取值范圍是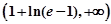 .
.
試題解析:(1)函數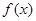 的定義域為
的定義域為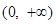 ,
,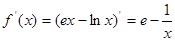 2分
2分
當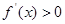 ,即
,即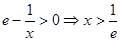 時,
時,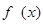 為單調遞增函數;
為單調遞增函數;
當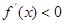 ,即
,即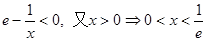 時,
時,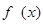 為單調遞減函數;
為單調遞減函數;
所以,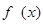 的單調遞增區間是
的單調遞增區間是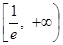 ,
,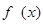 的單調遞減區間是
的單調遞減區間是 6分
6分
(2)由不等式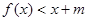 ,得
,得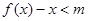 ,令
,令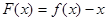 ,
,
則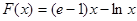 8分
8分
由題意可轉化為:在區間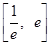 內,
內,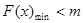 ,
,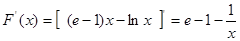 ,令
,令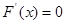 ,得
,得