
【題目】設P是不等式組  表示的平面區域內的任意一點,向量
表示的平面區域內的任意一點,向量 ![]() =(1,1),
=(1,1), ![]() =(2,1),若
=(2,1),若 ![]() =λ
=λ ![]() +μ
+μ ![]() (λ,μ為實數),則λ﹣μ的最大值為( )
(λ,μ為實數),則λ﹣μ的最大值為( )
A.4
B.3
C.﹣1
D.﹣2
科目:高中數學 來源: 題型:
【題目】如圖,在正方體![]() 中,若
中,若![]() 是線段
是線段![]() 上的動點,則下列結論不正確的是( )
上的動點,則下列結論不正確的是( )
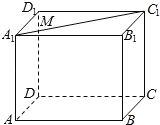
A. 三棱錐![]() 的正視圖面積是定值
的正視圖面積是定值
B. 異面直線![]() ,
,![]() 所成的角可為
所成的角可為![]()
C. 異面直線![]() ,
,![]() 所成的角為
所成的角為![]()
D. 直線![]() 與平面
與平面![]() 所成的角可為
所成的角可為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,過點
,過點![]() ,
,![]() 的直線傾斜角為
的直線傾斜角為![]() ,原點到該直線的距離為
,原點到該直線的距離為![]() .
.
(Ⅰ)求橢圓的標準方程;
(Ⅱ)斜率大于零的直線過![]() 與橢圓交于E,F兩點,若
與橢圓交于E,F兩點,若![]() ,求直線EF的方程.
,求直線EF的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》是我國古代數學名著,它在幾何學中的研究比西方造一千多年,例如塹堵指底面為直角三角形,且測量垂直底面的三棱柱,陽馬指底面為矩形,一側棱垂直于底面的四棱錐,如圖,在塹堵![]() 中,
中,![]() ,若當陽馬
,若當陽馬![]() 的體積最大時,則塹堵
的體積最大時,則塹堵![]() 的體積為__________
的體積為__________

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF ![]() 2CE,G是線段BF上一點,AB=AF=BC=2.
2CE,G是線段BF上一點,AB=AF=BC=2. 
(1)當GB=GF時,求證:EG∥平面ABC;
(2)求二面角E﹣BF﹣A的余弦值;
(3)是否存在點G滿足BF⊥平面AEG?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐P-ABCD中,側面PAD⊥底面ABCD,側棱PA=PD=![]() ,PA⊥PD,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O為AD中點.
,PA⊥PD,底面ABCD為直角梯形,其中BC∥AD,AB⊥AD,AB=BC=1,O為AD中點.
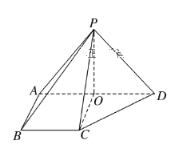
(1)求B點到平面PCD的距離;
(2)線段PD上是否存在一點Q,使得二面角Q-AC-D的余弦值為![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為  ( t為參數).以原點為極點,x軸正半軸為極軸 建立極坐標系,圓C的方程為 ρ=2
( t為參數).以原點為極點,x軸正半軸為極軸 建立極坐標系,圓C的方程為 ρ=2 ![]() sinθ.
sinθ.
(1)寫出直線l的普通方程和圓C的直角坐標方程;
(2)若點P的直角坐標為(1,0),圓C與直線l交于A,B兩點,求|PA|+|PB|的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com