
���}Ŀ����ֱ֪��![]() ��
��
��1�����C���oՓ![]() ȡ��ֵ��ֱ��
ȡ��ֵ��ֱ��![]() ʼ�K��(j��ng)�^��һ���ޣ�
ʼ�K��(j��ng)�^��һ���ޣ�
��2����ֱ��![]() �c
�c![]() �S�����S����
�S�����S����![]() �c(di��n)���c
�c(di��n)���c![]() �S�����S����
�S�����S����![]() �c(di��n)��
�c(di��n)��![]() ������(bi��o)ԭ�c(di��n)���O(sh��)
������(bi��o)ԭ�c(di��n)���O(sh��)![]() ����e��
����e��![]() ����
����![]() ����Сֵ���˕r(sh��)ֱ��
����Сֵ���˕r(sh��)ֱ��![]() �ķ��̣�
�ķ��̣�
���𰸡���1���C��Ҋ������ ��2����e![]() ����Сֵ��4��ֱ��
����Сֵ��4��ֱ��![]() �ķ��̞�
�ķ��̞�![]() ��
��
��������
��1���Ȍ�ֱ�����̻����c(di��n)бʽ�����![]() ��
��![]() ��ֵ���ɵö��c(di��n)����(bi��o)���ٸ���(j��)���c(di��n)�ڵ�һ���ޣ��ɵ�ֱ��
��ֵ���ɵö��c(di��n)����(bi��o)���ٸ���(j��)���c(di��n)�ڵ�һ���ޣ��ɵ�ֱ��![]() ʼ�K��(j��ng)�^��һ���ޣ�
ʼ�K��(j��ng)�^��һ���ޣ�
��2����һ�������![]() ��
��![]() ������(bi��o)���ɵ�
������(bi��o)���ɵ�![]() ����e��
����e��![]() ���_(d��)ʽ�������û�������ʽ�����
���_(d��)ʽ�������û�������ʽ�����![]() ����Сֵ���˕r(sh��)��
����Сֵ���˕r(sh��)��![]() ֵ���M(j��n)���õ��˕r(sh��)ֱ��
ֵ���M(j��n)���õ��˕r(sh��)ֱ��![]() �ķ��̣�
�ķ��̣�
�������O(sh��)ֱ���ķ��̞�![]()
![]() ���t
���t![]() ��ֱ��
��ֱ��![]() �^���c(di��n)
�^���c(di��n)![]() ������
������![]() �����û�������ʽ���
�����û�������ʽ���![]() ���t�ɵ�
���t�ɵ�![]() ����Сֵ���˕r(sh��)��
����Сֵ���˕r(sh��)��![]() ��ֵ���M(j��n)���õ��˕r(sh��)ֱ��
��ֵ���M(j��n)���õ��˕r(sh��)ֱ��![]() �ķ��̣�
�ķ��̣�
��1����?y��n)�ֱ��![]() ����
����![]() ����
����![]() �����
�����![]() ��
��![]() ��
��
��ֱ��![]() �^���c(di��n)
�^���c(di��n)![]() ���ڵ�һ���ޣ�
���ڵ�һ���ޣ�
���ԟoՓ![]() ȡ��ֵ��ֱ��
ȡ��ֵ��ֱ��![]() ʼ�K��(j��ng)�^��һ���ޣ�
ʼ�K��(j��ng)�^��һ���ޣ�
��2������һ����?y��n)�ֱ��![]() �c
�c![]() �S��
�S��![]() �S�����S�քe����
�S�����S�քe����![]() ��
��![]() ���c(di��n)������
���c(di��n)������![]() ��
��
��![]() �����
�����![]() ����
����![]() ����
����![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
�t![]() ��
��
��(d��ng)�҃H��(d��ng)![]() ��Ҳ��
��Ҳ��![]() �r(sh��)��ȡ�õ�̖(h��o)��
�r(sh��)��ȡ�õ�̖(h��o)��
�t![]() ��
��
��![]() ���Ķ�
���Ķ�![]() ����Сֵ��4��
����Сֵ��4��
�˕r(sh��)ֱ��![]() �ķ��̞�
�ķ��̞�![]() ����
����![]() ��
��
����������?y��n)�ֱ��![]() �c
�c![]() �S��
�S��![]() �S�����S�քe����
�S�����S�քe����![]() ��
��![]() ���c(di��n)���O(sh��)
���c(di��n)���O(sh��)![]() ��
��![]() ��
��
�O(sh��)ֱ���ķ��̞�![]()
![]() ���t
���t![]() ��
��
��ֱ��![]() �^���c(di��n)
�^���c(di��n)![]() ������
������![]() ��
��
����?y��n)?/span>![]() ��
��![]() ������
������![]() ��
��
����![]() ������
������![]() ��
��
��![]() ����
����![]() ����Сֵ��4��
����Сֵ��4��
�˕r(sh��)![]() �����
�����![]() ��
��![]() ��
��
����ֱ��![]() �ķ��̞�
�ķ��̞�![]() ������
������![]() ��
��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����˽�ij������(du��)�������_(t��i)������ُ��đB(t��i)�ȣ���ԓ���S�C(j��)��ȡ��50�������M(j��n)���{(di��o)�飬����?c��)����루��λ����Ԫ�����l��(sh��)�ֲ�����(du��)������ُ���ٝ���˔�(sh��)���±���
������ |
|
|
|
|
|
|
�l��(sh��) | 5 | 10 | 15 | 10 | 5 | 5 |
ٝ���˔�(sh��) | 4 | 8 | 8 | 5 | 2 | 1 |
�������벻����55��Ԫ����Ⱥ�Q�顰�������塱�����������55��Ԫ����Ⱥ�Q�顰�Ǹ������塱.
����
| 0.100 | 0.050 | 0.010 | 0.001 /td> |
| 2.706 | 3.841 | 6.635 | 10.828 |

�Ǹ������� | �������� | ��Ӌ(j��) | |
ٝ�� | |||
��ٝ�� | |||
��Ӌ(j��) |
��1������(j��)��֪�l����������![]() ��(li��n)�������Д��ж��İ����J(r��n)��ٝ��ٝ�ɘ�����ُ���c����ߵ����P(gu��n)��
��(li��n)�������Д��ж��İ����J(r��n)��ٝ��ٝ�ɘ�����ُ���c����ߵ����P(gu��n)��
��2���F(xi��n)����������![]() ����Ⱥ���S�C(j��)��ȡ���ˣ�������ȡ�ă�����������һ��ٝ�ɘ�����ُ��ĸ���.
����Ⱥ���S�C(j��)��ȡ���ˣ�������ȡ�ă�����������һ��ٝ�ɘ�����ُ��ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��
(1)��(d��ng)![]() �r(sh��)��ӑՓ����(sh��)
�r(sh��)��ӑՓ����(sh��)![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
(2)��(sh��)![]() �ĘOֵ.
�ĘOֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�������ĽM����(sh��)�У���ʾͬһ����(sh��)����
A.f��x��=![]()
![]() ��g��x��=x2�C1B.f��x��=
��g��x��=x2�C1B.f��x��=![]() ��g��x��=x+1
��g��x��=x+1
C.f��x��=![]() ��g��x��=��
��g��x��=��![]() ��2D.f��x��=|x|��g��t��=
��2D.f��x��=|x|��g��t��=![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����������߅![]() ��
��![]() ��
��![]() ��߅����������������
��߅����������������![]() ��
��![]() ��
��![]() ���t
���t![]() ��
��![]() ��
��![]() �������c(di��n)��ԓ�c(di��n)�Q��
�������c(di��n)��ԓ�c(di��n)�Q��![]() �����Ƚ����ģ���(d��ng)
�����Ƚ����ģ���(d��ng)![]() ��ÿ��(g��)��(n��i)�Ƕ�С��120�r(sh��)�����Ƚ������c(di��n)P�M���������|(zh��)��
��ÿ��(g��)��(n��i)�Ƕ�С��120�r(sh��)�����Ƚ������c(di��n)P�M���������|(zh��)��
��1��![]() ����2�����Ƚ������ǵ�ԓ����������(g��)��c(di��n)���x֮����С���c(di��n)��Ҳ���M(f��i)�R�c(di��n)�������������|(zh��)��
����2�����Ƚ������ǵ�ԓ����������(g��)��c(di��n)���x֮����С���c(di��n)��Ҳ���M(f��i)�R�c(di��n)�������������|(zh��)��![]() ����Сֵ��_________
����Сֵ��_________
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����P(y��ng)�����Ļ���ij�W(xu��)У�W(xu��)��ȫ�T���c�e�������Ґۇ��W(xu��)�����b��(j��ng)������ԇ�������г�ȡ![]() ���W(xu��)���ijɿ����ٷ��ƣ�����ӱ����õ��l�ʷֲ�ֱ���D��D��ʾ���ɿ�����
���W(xu��)���ijɿ����ٷ��ƣ�����ӱ����õ��l�ʷֲ�ֱ���D��D��ʾ���ɿ�����![]() �е��˔�(sh��)��20��
�е��˔�(sh��)��20��

��1����![]() ��
��![]() ��ֵ��
��ֵ��
��2������(j��)�ӱ���Ӌ(j��)���w��˼�룬��Ӌ(j��)ԓУ�W(xu��)����(sh��)�W(xu��)�ɿ���ƽ����(sh��)![]() ����λ��(sh��)
����λ��(sh��)![]() ����ͬһ�M��(sh��)��(j��)�еĔ�(sh��)��(j��)���@�M��(sh��)��(j��)���څ^(q��)�g���c(di��n)��ֵ��������
����ͬһ�M��(sh��)��(j��)�еĔ�(sh��)��(j��)���@�M��(sh��)��(j��)���څ^(q��)�g���c(di��n)��ֵ��������
��3�����ɿ�?c��)?/span>80�����ϣ���80�֣��������W(xu��)С�_(d��)���������ژӱ��У����÷ӳ�ӵķ����������W(xu��)С�_(d��)�������S�C(j��)��ȡ5�ˣ��ُ��г�ȡ2��ٛ(z��ng)��һ�ׇ��W(xu��)��(j��ng)�䣬ӛ�����е�2���W(xu��)���ɿ���������90�������¼�![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪����![]() �ĘO����(bi��o)������
�ĘO����(bi��o)������![]() .�ԘO�c(di��n)��ƽ��ֱ������(bi��o)ϵ��ԭ�c(di��n)���O�S��
.�ԘO�c(di��n)��ƽ��ֱ������(bi��o)ϵ��ԭ�c(di��n)���O�S��![]() �S�������S������ƽ��ֱ������(bi��o)ϵ��ֱ��
�S�������S������ƽ��ֱ������(bi��o)ϵ��ֱ��![]() �ą���(sh��)������
�ą���(sh��)������![]() ��
��![]() �酢��(sh��)��.
�酢��(sh��)��.
��������![]() �ĘO����(bi��o)���̻���ֱ������(bi��o)���̣�
�ĘO����(bi��o)���̻���ֱ������(bi��o)���̣�
������ֱ��![]() �c����
�c����![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ����ֱ��
����ֱ��![]() �ăAб��
�ăAб��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��ijȺ�w���˾�ͨ�ڕr(sh��)�g����ָ���Ճ�(n��i)ԓȺ�w�гɆT�ľ�ס�ص������ص�ƽ���Õr(sh��)��ij���ϰ���![]() �еijɆT�H�����{����ʽͨ�ڣ������@ʾ����(d��ng)
�еijɆT�H�����{����ʽͨ�ڣ������@ʾ����(d��ng)![]() ��
��![]() ��
��![]() ���ijɆT���{�r(sh��)�����{Ⱥ�w���˾�ͨ�ڕr(sh��)�g��
���ijɆT���{�r(sh��)�����{Ⱥ�w���˾�ͨ�ڕr(sh��)�g�� ����λ����犣���������Ⱥ�w���˾�ͨ�ڕr(sh��)�g����
����λ����犣���������Ⱥ�w���˾�ͨ�ڕr(sh��)�g����![]() Ӱ푣����
Ӱ푣����![]() ��犣�ԇ����(j��)���������Y(ji��)���ش����І��}��
��犣�ԇ����(j��)���������Y(ji��)���ش����І��}��
��1����(d��ng)![]() ��ʲô������(n��i)�r(sh��)������Ⱥ�w���˾�ͨ�ڕr(sh��)�g�������{Ⱥ�w���˾�ͨ�ڕr(sh��)�g��
��ʲô������(n��i)�r(sh��)������Ⱥ�w���˾�ͨ�ڕr(sh��)�g�������{Ⱥ�w���˾�ͨ�ڕr(sh��)�g��
��2����ԓ���ϰ���![]() ���˾�ͨ�ڕr(sh��)�g
���˾�ͨ�ڕr(sh��)�g![]() �ı��_(d��)ʽ��ӑՓ
�ı��_(d��)ʽ��ӑՓ![]() �Ć��{(di��o)�ԣ����f���䌍(sh��)�H���x��
�Ć��{(di��o)�ԣ����f���䌍(sh��)�H���x��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
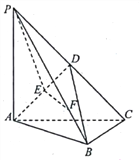
���}Ŀ����D���������F![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() �����c(di��n)��
�����c(di��n)��![]() ��
��![]() �����c(di��n)���c(di��n)
�����c(di��n)���c(di��n)![]() �ھ���
�ھ���![]() �ϣ�
�ϣ�![]() ��
��![]() .
.
�������C��![]() ƽ��
ƽ��![]() ��
��
������![]() �����C��
�����C��![]() ƽ��
ƽ��![]() ��
��
������![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com