
已知函數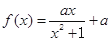 ,
,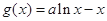 (
(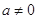 ).
).
(1)求函數 的單調區間;
的單調區間;
(2)求證:當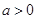 時,對于任意
時,對于任意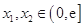 ,總有
,總有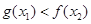 成立.
成立.
(1)當 時,
時, 的單調遞增區間為
的單調遞增區間為 ,單調遞減區間為
,單調遞減區間為 ,
, ;當
;當 時,
時, 的單調遞增區間為
的單調遞增區間為 ,
, ,單調遞減區間為
,單調遞減區間為 ;(2)詳見解析.
;(2)詳見解析.
解析試題分析:(1)對于含參數的函數的單調區間,只需在定義域內考慮導函數符號,同時要注意分類討論標準的確定.先求 ,分母恒正,只需考慮分子二次函數的符號,所以討論開口方向即可;(2)由于
,分母恒正,只需考慮分子二次函數的符號,所以討論開口方向即可;(2)由于 是獨立的兩個變量,故
是獨立的兩個變量,故 分別代表
分別代表 ,
, 的任意兩個函數值,要使得
的任意兩個函數值,要使得 恒成立,只需證明
恒成立,只需證明 ,分別利用導數求其最大值和最小值,從而得證,該題入手,可能很多同學困惑于
,分別利用導數求其最大值和最小值,從而得證,該題入手,可能很多同學困惑于 這兩個變量的處理,從而造成了解題障礙.
這兩個變量的處理,從而造成了解題障礙.
試題解析:(Ⅰ)函數 的定義域為
的定義域為 ,
, .
.
當 時,
時,
當 變化時,
變化時, ,
, 的變化情況如下表:
的變化情況如下表:
當







0 
0 

↘ ↗ ↘  時,
時,
當 變化時,
變化時, ,
, 的變化情況如下表:
的變化情況如下表: