
【題目】在直角坐標系xOy中,以坐標原點為極點,x軸的非負半軸為極軸建立極坐標系;曲線C1的普通方程為(x-1)2 +y2 =1,曲線C2的參數方程為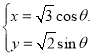 (θ為參數).
(θ為參數).
(Ⅰ)求曲線C1和C2的極坐標方程:
(Ⅱ)設射線θ=![]() (ρ>0)分別與曲線C1和C2相交于A,B兩點,求|AB|的值.
(ρ>0)分別與曲線C1和C2相交于A,B兩點,求|AB|的值.
 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】如圖,湖中有一個半徑為![]() 千米的圓形小島,岸邊點
千米的圓形小島,岸邊點![]() 與小島圓心
與小島圓心![]() 相距
相距![]() 千米,為方便游人到小島觀光,從點
千米,為方便游人到小島觀光,從點![]() 向小島建三段棧道
向小島建三段棧道![]() ,
,![]() ,
,![]() ,湖面上的點
,湖面上的點![]() 在線段
在線段![]() 上,且
上,且![]() ,
,![]() 均與圓
均與圓![]() 相切,切點分別為
相切,切點分別為![]() ,
,![]() ,其中棧道
,其中棧道![]() ,
,![]() ,
,![]() 和小島在同一個平面上.沿圓
和小島在同一個平面上.沿圓![]() 的優弧(圓
的優弧(圓![]() 上實線部分)上再修建棧道
上實線部分)上再修建棧道![]() .記
.記![]() 為
為![]() .
.
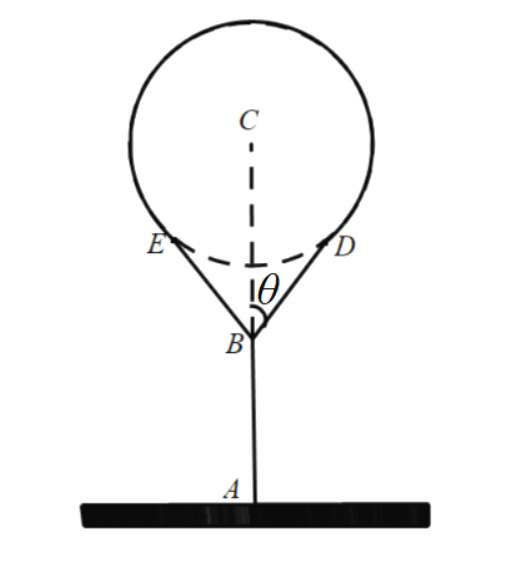
![]() 用
用![]() 表示棧道的總長度
表示棧道的總長度![]() ,并確定
,并確定![]() 的取值范圍;
的取值范圍;
![]() 求當
求當![]() 為何值時,棧道總長度最短.
為何值時,棧道總長度最短.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在綜合素質評價的某個維度的測評中,依據評分細則,學生之間相互打分,最終將所有的數據合成一個分數,滿分100分,按照大于或等于80分的為優秀,小于80分的為合格,為了解學生的在該維度的測評結果,在畢業班中隨機抽出一個班的數據.該班共有60名學生,得到如下的列聯表:
優秀 | 合格 | 總計 | |
男生 | 6 | ||
女生 | 18 | ||
合計 | 60 |
已知在該班隨機抽取1人測評結果為優秀的概率為![]() .
.
(1)完成上面的列聯表;
(2)能否在犯錯誤的概率不超過0.10的前提下認為性別與測評結果有關系?
(3)現在如果想了解全校學生在該維度的表現情況,采取簡單隨機抽樣方式在全校學生中抽取少數一部分來分析,請你選擇一個合適的抽樣方法,并解釋理由.
附: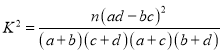
| 0.25 | 0.10 | 0.025 |
| 1.323 | 2.706 | 5.024 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某省從2021年開始將全面推行新高考制度,新高考“![]() ”中的“2”要求考生從政治、化學、生物、地理四門中選兩科,按照等級賦分計入高考成績,等級賦分規則如下:從2021年夏季高考開始,高考政治、化學、生物、地理四門等級考試科目的考生原始成績從高到低劃分為
”中的“2”要求考生從政治、化學、生物、地理四門中選兩科,按照等級賦分計入高考成績,等級賦分規則如下:從2021年夏季高考開始,高考政治、化學、生物、地理四門等級考試科目的考生原始成績從高到低劃分為![]() 五個等級,確定各等級人數所占比例分別為
五個等級,確定各等級人數所占比例分別為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,等級考試科目成績計入考生總成績時,將
,等級考試科目成績計入考生總成績時,將![]() 至
至![]() 等級內的考生原始成績,依照等比例轉換法分別轉換到
等級內的考生原始成績,依照等比例轉換法分別轉換到![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五個分數區間,得到考生的等級分,等級轉換分滿分為100分.具體轉換分數區間如下表:
五個分數區間,得到考生的等級分,等級轉換分滿分為100分.具體轉換分數區間如下表:
等級 |
|
|
|
|
|
比例 |
|
|
|
|
|
賦分區間 |
|
|
|
|
|
而等比例轉換法是通過公式計算:![]()
其中![]() ,
,![]() 分別表示原始分區間的最低分和最高分,
分別表示原始分區間的最低分和最高分,![]() 、
、![]() 分別表示等級分區間的最低分和最高分,
分別表示等級分區間的最低分和最高分,![]() 表示原始分,
表示原始分,![]() 表示轉換分,當原始分為
表示轉換分,當原始分為![]() ,
,![]() 時,等級分分別為
時,等級分分別為![]() 、
、![]()
假設小南的化學考試成績信息如下表:
考生科目 | 考試成績 | 成績等級 | 原始分區間 | 等級分區間 |
化學 | 75分 |
|
|
|
設小南轉換后的等級成績為![]() ,根據公式得:
,根據公式得:![]() ,
,
所以![]() (四舍五入取整),小南最終化學成績為77分.
(四舍五入取整),小南最終化學成績為77分.
已知某年級學生有100人選了化學,以半期考試成績為原始成績轉換本年級的化學等級成績,其中化學成績獲得![]() 等級的學生原始成績統計如下表:
等級的學生原始成績統計如下表:
成績 | 95 | 93 | 91 | 90 | 88 | 87 | 85 |
人數 | 1 | 2 | 3 | 2 | 3 | 2 | 2 |
(1)從化學成績獲得![]() 等級的學生中任取2名,求恰好有1名同學的等級成績不小于96分的概率;
等級的學生中任取2名,求恰好有1名同學的等級成績不小于96分的概率;
(2)從化學成績獲得![]() 等級的學生中任取5名,設5名學生中等級成績不小于96分人數為
等級的學生中任取5名,設5名學生中等級成績不小于96分人數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2013年至201 9年我國二氧化硫的年排放量(單位:萬噸)如下表,則以下結論中錯誤的是( )
![]()
A.二氧化硫排放量逐年下降
B.2018年二氧化硫減排效果最為顯著
C.2017年至2018年二氧化硫減排量比2013年至2016年二氧化硫減排量的總和大
D.2019年二氧化硫減排量比2018年二氧化硫減排量有所增加
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一年之計在于春,一日之計在于晨,春天是播種的季節,是希望的開端.某種植戶對一塊地的![]() 個坑進行播種,每個坑播3粒種子,每粒種子發芽的概率均為
個坑進行播種,每個坑播3粒種子,每粒種子發芽的概率均為![]() ,且每粒種子是否發芽相互獨立.對每一個坑而言,如果至少有兩粒種子發芽,則不需要進行補播種,否則要補播種.
,且每粒種子是否發芽相互獨立.對每一個坑而言,如果至少有兩粒種子發芽,則不需要進行補播種,否則要補播種.
(1)當![]() 取何值時,有3個坑要補播種的概率最大?最大概率為多少?
取何值時,有3個坑要補播種的概率最大?最大概率為多少?
(2)當![]() 時,用
時,用![]() 表示要補播種的坑的個數,求
表示要補播種的坑的個數,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在開展學習強國的活動中,某校高三數學教師成立了黨員和非黨員兩個學習組,其中黨員學習組有4名男教師、1名女教師,非黨員學習組有2名男教師、2名女教師,高三數學組計劃從兩個學習組中隨機各選2名教師參加學校的挑戰答題比賽.
(1)求選出的4名選手中恰好有一名女教師的選派方法數;
(2)記X為選出的4名選手中女教師的人數,求X的概率分布和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據氣象部門預報,在距離某個碼頭A南偏東45°方向的600km處的熱帶風暴中心B正以30km/h的速度向正北方向移動,距離風暴中心450km以內的地區都將受到影響,從現在起經過___小時后該碼頭A將受到熱帶風暴的影響(精確到0.01).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動圓過定點![]() ,且與直線
,且與直線![]() 相切,動圓圓心的軌跡為
相切,動圓圓心的軌跡為![]() ,過
,過![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 與
與![]() 交于兩點
交于兩點![]() ,過
,過![]() 分別作
分別作![]() 的切線,兩切線的交點為
的切線,兩切線的交點為![]() ,直線
,直線![]() 與
與![]() 交于兩點
交于兩點![]() .
.
(1)證明:點![]() 始終在直線
始終在直線![]() 上且
上且![]() ;
;
(2)求四邊形![]() 的面積的最小值.
的面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com