
【題目】設(shè)直線![]() 與拋物線
與拋物線![]() 相交于不同兩點
相交于不同兩點![]() 、
、![]() ,
, ![]() 為坐標(biāo)原點.
為坐標(biāo)原點.
(1)求拋物線![]() 的焦點到準(zhǔn)線的距離;
的焦點到準(zhǔn)線的距離;
(2)若直線![]() 又與圓
又與圓![]() 相切于點
相切于點![]() ,且
,且![]() 為線段
為線段![]() 的中點,求直線
的中點,求直線![]() 的方程;
的方程;
(3)若![]() ,點
,點![]() 在線段
在線段![]() 上,滿足
上,滿足![]() ,求點
,求點![]() 的軌跡方程.
的軌跡方程.
【答案】(1)2;(2)![]() ,
, ![]() ;(3)
;(3)![]()
【解析】試題分析:(1)根據(jù)題意,由拋物線的方程分析可得![]() 的值,即可得答案;(2)根據(jù)題意,設(shè)直線
的值,即可得答案;(2)根據(jù)題意,設(shè)直線![]() 的方程為
的方程為![]() ,分
,分![]() 與
與![]() 兩種情況討論,分析
兩種情況討論,分析![]() 的取值,綜合可得
的取值,綜合可得![]() 可取的值,將
可取的值,將![]() 的值代入直線的方程即可得答案;(3)設(shè)直線
的值代入直線的方程即可得答案;(3)設(shè)直線![]() ,設(shè)
,設(shè)![]() 、
、![]() ,將直線的方程與拋物線方程聯(lián)立,結(jié)合
,將直線的方程與拋物線方程聯(lián)立,結(jié)合![]() ,由根與系數(shù)的關(guān)系分析可得答案.
,由根與系數(shù)的關(guān)系分析可得答案.
試題解析:(1)∵拋物線![]() 的方程為
的方程為![]()
∴拋物線![]() 的焦點到準(zhǔn)線的距離為2
的焦點到準(zhǔn)線的距離為2
(2)設(shè)直線![]()
當(dāng)![]() 時,
時, ![]() 和
和![]() 符合題意;
符合題意;
當(dāng)![]() 時,
時, ![]() 、
、![]() 的坐標(biāo)滿足方程組
的坐標(biāo)滿足方程組![]() ,
,
∴![]() 的兩根為
的兩根為![]() 、
、![]() ,
, ![]() ,
, ![]()
∴![]() ,
,
∴線段![]() 的中點
的中點![]()
∵![]() ,
, ![]()
∴![]() ,得
,得![]()
∴![]() ,得
,得![]()
∵![]()
∴![]() (舍去)
(舍去)
綜上所述,直線![]() 的方程為:
的方程為: ![]() ,
, ![]()
(3)設(shè)直線![]() ,
,
![]() 、
、![]() 的坐標(biāo)滿足方程組
的坐標(biāo)滿足方程組![]() ,
,
∴![]() 的兩根為
的兩根為![]() 、
、![]()
![]() ,
, ![]() ,
, ![]()
∴![]() ,得
,得![]() 或
或![]()
![]() 時,直線AB過原點,所以
時,直線AB過原點,所以![]() ;
;
![]() 時,直線AB過定點
時,直線AB過定點![]()
設(shè)![]()
∵![]() ,
,
∴![]() (
(![]() ),
),
綜上,點![]() 的軌跡方程為
的軌跡方程為![]()


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學(xué)業(yè)考試導(dǎo)與練系列答案
初中學(xué)業(yè)考試導(dǎo)與練系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知 ![]() 為坐標(biāo)原點,
為坐標(biāo)原點, ![]() ,
, ![]() 是橢圓
是橢圓 ![]() 上的點,且
上的點,且 ![]() ,設(shè)動點
,設(shè)動點 ![]() 滿足
滿足 ![]() .
.
(Ⅰ)求動點 ![]() 的軌跡
的軌跡 ![]() 的方程;
的方程;
(Ⅱ)若直線 ![]() 與曲線
與曲線 ![]() 交于
交于 ![]() 兩點,求三角形
兩點,求三角形 ![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某企業(yè)為了對新研發(fā)的一批產(chǎn)品進行合理定價,將產(chǎn)品按事先擬定的價格進行試銷,得到一組銷售數(shù)據(jù)![]() ,如表所示:
,如表所示:

已知![]()
(1)求![]() 的值
的值
(2)已知變量![]() 具有線性相關(guān)性,求產(chǎn)品銷量
具有線性相關(guān)性,求產(chǎn)品銷量![]() 關(guān)于試銷單價
關(guān)于試銷單價![]() 的線性回歸方程
的線性回歸方程![]() 可供選擇的數(shù)據(jù)
可供選擇的數(shù)據(jù)![]()
(3)用![]() 表示(2)中所求的線性回歸方程得到的與
表示(2)中所求的線性回歸方程得到的與![]() 對應(yīng)的產(chǎn)品銷量的估計值。當(dāng)銷售數(shù)據(jù)
對應(yīng)的產(chǎn)品銷量的估計值。當(dāng)銷售數(shù)據(jù)![]() 對應(yīng)的殘差的絕對值
對應(yīng)的殘差的絕對值![]() 時,則將銷售數(shù)據(jù)
時,則將銷售數(shù)據(jù)![]() 稱為一個“好數(shù)據(jù)”。試求這6組銷售數(shù)據(jù)中的 “好數(shù)據(jù)”。
稱為一個“好數(shù)據(jù)”。試求這6組銷售數(shù)據(jù)中的 “好數(shù)據(jù)”。
參考數(shù)據(jù):線性回歸方程中![]() 的最小二乘估計分別是
的最小二乘估計分別是
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,三個函數(shù)的定義域均為集合
,三個函數(shù)的定義域均為集合![]() .
.
(1)若![]() 恒成立,滿足條件的實數(shù)
恒成立,滿足條件的實數(shù)![]() 組成的集合為
組成的集合為![]() ,試判斷集合
,試判斷集合![]() 與
與![]() 的關(guān)系,并說明理由;
的關(guān)系,并說明理由;
(2)記 ,是否存在
,是否存在![]() ,使得對任意的實數(shù)
,使得對任意的實數(shù)![]() ,函數(shù)
,函數(shù)![]() 有且僅有兩個零點?若存在,求出滿足條件的最小正整數(shù)
有且僅有兩個零點?若存在,求出滿足條件的最小正整數(shù)![]() ;若不存在,說明理由.(以下數(shù)據(jù)供參考:
;若不存在,說明理由.(以下數(shù)據(jù)供參考: ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,公園有一塊邊長為2的等邊△ABC的邊角地,現(xiàn)修成草坪,圖中DE把草坪分成面積相等的兩部分,D在AB上,E在AC上.
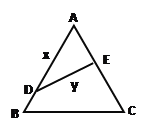
(1)設(shè)AD=x(x≥1),ED=y,求用x表示y的函數(shù)關(guān)系式;
(2)如果DE是灌溉水管,為節(jié)約成本,希望它最短,DE的位置應(yīng)在哪里?如果DE是參觀線路,則希望它最長,DE的位置又應(yīng)在哪里?請予證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】韓國民意調(diào)查機構(gòu)“蓋洛普韓國”2016年11月公布的民調(diào)結(jié)果顯示,受“閨蜜門”時間影響,韓國總統(tǒng)樸槿惠的民意支持率持續(xù)下跌,在所調(diào)查的1000個對象中,年齡在[20,30)的群體有200人,支持率為0%,年齡在[30,40)和[40,50)的群體中,支持率均為3%;年齡在[50,60)和[60,70)的群體中,支持率分別為6%和13%,若在調(diào)查的對象中,除[20,30)的群體外,其余各年齡層的人數(shù)分布情況如頻率分布直方圖所示,其中最后三組的頻數(shù)構(gòu)成公差為100的等差數(shù)列.
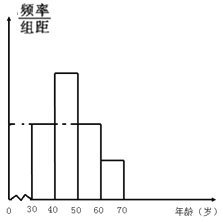
(1)依頻率分布直方圖求出圖中各年齡層的人數(shù)
(2)請依上述支持率完成下表:
年齡分布 是否支持 | [30,40)和[40,50) | [50,60)和[60,70) | 合計 |
支持 | |||
不支持 | |||
合計 |
根據(jù)表中的數(shù)據(jù),能否在犯錯誤的概率不超過0.001的前提下認(rèn)為年齡與支持率有關(guān)?
附表:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式:![]() ,其中
,其中![]() 參考數(shù)據(jù):125×33=15×275,125×97=25×485)
參考數(shù)據(jù):125×33=15×275,125×97=25×485)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
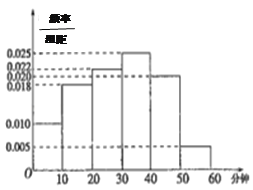
【題目】電視傳媒公司為了解某地區(qū)電視觀眾對某類體育節(jié)目的收視情況,隨機抽取了100名觀眾進行調(diào)查.下面是根據(jù)調(diào)查結(jié)果繪制的觀眾日均收看該體育節(jié)目時間的頻率分布直方圖:
非體育迷 | 體育迷 | 合計 | |
男 | |||
女 | 10 | 55 | |
合計 |
將日均收看該體育節(jié)目時間不低于40分鐘的觀眾稱為“體育迷”.
(1)根據(jù)已知條件完成上面的2×2列聯(lián)表,若按95%的可靠性要求,并據(jù)此資料,你是否認(rèn)為“體育迷”與性別有關(guān)?
(2)現(xiàn)在從該地區(qū)非體育迷的電視觀眾中,采用分層抽樣方法選取5名觀眾,求從這5名觀眾選取兩人進行訪談,被抽取的2名觀眾中至少有一名女生的概率.
附:![]()
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知長方形![]() 中,
中,![]() ,
,![]() ,M為DC的中點.將
,M為DC的中點.將![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() ⊥平面
⊥平面![]() .
.
(1)求證:![]() ;
;
(2)若點![]() 是線段
是線段![]() 上的一動點,問點
上的一動點,問點![]() 在何位置時,二面角
在何位置時,二面角![]() 的余弦值為
的余弦值為![]() .
.


查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com