
【題目】若函數(shù)![]() 對定義域內(nèi)的每一個值
對定義域內(nèi)的每一個值![]() ,在其定義域內(nèi)都存在唯一的
,在其定義域內(nèi)都存在唯一的![]() ,使
,使![]() 成立,則稱該函數(shù)為“依賴函數(shù)”.
成立,則稱該函數(shù)為“依賴函數(shù)”.
(1)判斷函數(shù)![]() 是否為“依賴函數(shù)”,并說明理由;
是否為“依賴函數(shù)”,并說明理由;
(2)若函數(shù)![]() 在定義域
在定義域![]() (
(![]() )上為“依賴函數(shù)”,求
)上為“依賴函數(shù)”,求![]() 的取值范圍;
的取值范圍;
(3)已知函數(shù)![]() 在定義域
在定義域![]() 上為“依賴函數(shù)”.若存在實數(shù)
上為“依賴函數(shù)”.若存在實數(shù)![]() ,使得對任意的
,使得對任意的![]() ,不等式
,不等式![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的最大值.
的最大值.
【答案】(1)不是“依賴函數(shù)”,見解析;(2)![]() (3)實數(shù)
(3)實數(shù)![]() 的最大值為
的最大值為![]() .
.
【解析】
(1)利用![]() 時,
時,![]() 不可能成立,判斷出
不可能成立,判斷出![]() 不是“依賴函數(shù)”.
不是“依賴函數(shù)”.
(2)結(jié)合指數(shù)型函數(shù)的單調(diào)性,利用“依賴函數(shù)”的定義,求得![]() ,由此將
,由此將![]() 轉(zhuǎn)化為
轉(zhuǎn)化為![]() ,然后結(jié)合二次函數(shù)的單調(diào)性,求得
,然后結(jié)合二次函數(shù)的單調(diào)性,求得![]() 的取值范圍.
的取值范圍.
(3)根據(jù)![]() 與區(qū)間
與區(qū)間![]() 的位置關系進行分類討論,結(jié)合二次函數(shù)的性質(zhì)以及“依賴函數(shù)”的定義,求得
的位置關系進行分類討論,結(jié)合二次函數(shù)的性質(zhì)以及“依賴函數(shù)”的定義,求得![]() 的值.由此化簡不等式
的值.由此化簡不等式![]() 為以
為以![]() 為主變量的形式.利用判別式得到
為主變量的形式.利用判別式得到![]() ,結(jié)合存在性問題,由
,結(jié)合存在性問題,由![]() 的最大值,求得
的最大值,求得![]() 的取值范圍,從而求得
的取值范圍,從而求得![]() 的最大值.
的最大值.
(1)對于函數(shù)![]() 的定義域
的定義域![]() 內(nèi)存在
內(nèi)存在![]() ,
,
則![]() ,無解,故
,無解,故![]() 不是“依賴函數(shù)”.
不是“依賴函數(shù)”.
(2)因為![]() 在
在![]() 遞增,故
遞增,故![]() ,即
,即![]() ,
,![]()
由![]() ,故
,故![]() ,得
,得![]() ,
,
從而![]() 在
在![]() 上單調(diào)遞增,故
上單調(diào)遞增,故![]() ,
,
(3)①若![]() ,故
,故![]() 在
在![]() 上最小值為0,此時不存在
上最小值為0,此時不存在![]() ,舍去;
,舍去;
②若![]() 故
故![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
∴![]() ,解得
,解得![]() (舍)或
(舍)或![]() .
.
∴存在![]() ,使得對任意的
,使得對任意的![]() ,有不等式
,有不等式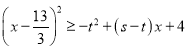 都成立,
都成立,
即![]() 恒成立,由
恒成立,由![]() ,
,
得![]() ,由
,由![]() ,可得
,可得![]() ,
,
又![]() 在
在![]() 單調(diào)遞減,故當
單調(diào)遞減,故當![]() 時,
時,![]() ,
,
從而![]() ,解得
,解得![]() ,
,
綜上,故實數(shù)![]() 的最大值為
的最大值為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】某校“凌云杯”籃球隊的成員來自學校高一、高二共10個班的12位同學,其中高一(3)班、高二(3)各出2人,其余班級各出1人,這12人中要選6人為主力隊員,則這6人來自不同的班級的概率為_____.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知![]() ,B為AC的中點,分別以AB,AC為直徑在AC的同側(cè)作半圓,M,N分別為兩半圓上的動點
,B為AC的中點,分別以AB,AC為直徑在AC的同側(cè)作半圓,M,N分別為兩半圓上的動點![]() 不含端點A,B,
不含端點A,B,![]() ,且
,且![]() ,則
,則![]() 的最大值為______.
的最大值為______.

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知變量![]() 、
、![]() 之間的線性回歸方程為
之間的線性回歸方程為![]() ,且變量
,且變量![]() 、
、![]() 之間的一-組相關數(shù)據(jù)如下表所示,則下列說法錯誤的是( )
之間的一-組相關數(shù)據(jù)如下表所示,則下列說法錯誤的是( )
|
|
|
|
|
|
|
|
|
|
A.可以預測,當![]() 時,
時,![]() B.
B.![]()
C.變量![]()
![]() 之間呈負相關關系D.該回歸直線必過點
之間呈負相關關系D.該回歸直線必過點![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在正方體ABCD﹣A1B1C1D1中,E是棱CC1的中點,F是側(cè)面BCC1B1內(nèi)的動點,且A1F∥平面D1AE,記A1F與平面BCC1B1所成的角為θ,下列說法正確的個數(shù)是( )
①點F的軌跡是一條線段
②A1F與D1E不可能平行
③A1F與BE是異面直線
④![]()
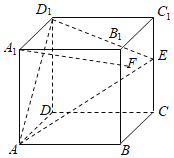
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,某人工景觀湖外圍有兩條相互垂直的直線型公路ll,l2,且ll和l2交于點O.為了方便游客游覽,計劃修建一條連接公路與景觀湖的直線型公路AB.景觀湖的輪廓可以近似看成一個圓心為O,半徑為2百米的圓,且公路AB與圓O相切,圓心O到ll,l2的距離均為5百米,設OAB=![]() ,AB長為L百米.
,AB長為L百米.
(1)求L關于![]() 的函數(shù)解析式;
的函數(shù)解析式;
(2)當![]() 為何值時,公路AB的長度最短?
為何值時,公路AB的長度最短?

查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知f(x)是定義在![]() 上的單調(diào)函數(shù),且對任意的x∈
上的單調(diào)函數(shù),且對任意的x∈![]() 都有
都有![]() ,則方程
,則方程![]() 的一個根所在的區(qū)間是( )
的一個根所在的區(qū)間是( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某大學生從全校學生中隨機選取![]() 名統(tǒng)計他們的鞋碼大小,得到如下數(shù)據(jù):
名統(tǒng)計他們的鞋碼大小,得到如下數(shù)據(jù):
鞋碼 |
|
|
|
|
|
|
|
|
|
| 合計 |
男生 |
|
|
|
|
|
|
|
|
| ||
女生 |
|
|
|
|
|
|
|
|
|
以各性別各鞋碼出現(xiàn)的頻率為概率.
(![]() )從該校隨機挑選一名學生,求他(她)的鞋碼為奇數(shù)的概率.
)從該校隨機挑選一名學生,求他(她)的鞋碼為奇數(shù)的概率.
(![]() )為了解該校學生考試作弊的情況,從該校隨機挑選
)為了解該校學生考試作弊的情況,從該校隨機挑選![]() 名學生進行抽樣調(diào)查.每位學生從裝有除顏色外無差別的
名學生進行抽樣調(diào)查.每位學生從裝有除顏色外無差別的![]() 個紅球和
個紅球和![]() 個白球的口袋中,隨機摸出兩個球,若同色,則如實回答其鞋碼是否為奇數(shù);若不同色,則如實回答是否曾在考試中作弊.這里的回答,是指在紙上寫下“是”或“否”.若調(diào)查人員回收到
個白球的口袋中,隨機摸出兩個球,若同色,則如實回答其鞋碼是否為奇數(shù);若不同色,則如實回答是否曾在考試中作弊.這里的回答,是指在紙上寫下“是”或“否”.若調(diào)查人員回收到![]() 張“是”的小紙條,試估計該校學生在考試中曾有作弊行為的概率.
張“是”的小紙條,試估計該校學生在考試中曾有作弊行為的概率.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com