
【題目】如圖,某人在垂直于水平地面ABC的墻面前的點(diǎn)A處進(jìn)行射擊訓(xùn)練.已知點(diǎn)A到墻面的距離為AB,某目標(biāo)點(diǎn)P沿墻面上的射線(xiàn)CM移動(dòng),此人為了準(zhǔn)確瞄準(zhǔn)目標(biāo)點(diǎn)P,需計(jì)算由點(diǎn)A觀察點(diǎn)P的仰角θ的大小.若AB=15m,AC=25m,∠BCM=30°,則tanθ的最大值是 . (仰角θ為直線(xiàn)AP與平面ABC所成角) 
【答案】![]()
【解析】解:∵AB=15m,AC=25m,∠ABC=90°,
∴BC=20m,
過(guò)P作PP′⊥BC,交BC于P′,連接AP′,則tanθ= ![]() ,
,
設(shè)BP′=x,則CP′=20﹣x,
由∠BCM=30°,得PP′=CP′tan30°= ![]() (20﹣x),
(20﹣x),
在直角△ABP′中,AP′= ![]() ,
,
∴tanθ= ![]()
![]() ,
,
令y= ![]() ,則函數(shù)在x∈[0,20]單調(diào)遞減,
,則函數(shù)在x∈[0,20]單調(diào)遞減,
∴x=0時(shí),取得最大值為 ![]() =
= ![]() .
.
若P′在CB的延長(zhǎng)線(xiàn)上,PP′=CP′tan30°= ![]() (20+x),
(20+x),
在直角△ABP′中,AP′= ![]() ,
,
∴tanθ= ![]()
![]() ,
,
令y= ![]() ,則y′=0可得x=
,則y′=0可得x= ![]() 時(shí),函數(shù)取得最大值
時(shí),函數(shù)取得最大值 ![]() ,
,
所以答案是: ![]() .
.


 名校課堂系列答案
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】求滿(mǎn)足下列條件的直線(xiàn)方程.
(1)經(jīng)過(guò)點(diǎn)A(-1,-3),且斜率等于直線(xiàn)3x+8y-1=0斜率的2倍;
(2)過(guò)點(diǎn)M(0,4),且與兩坐標(biāo)軸圍成三角形的周長(zhǎng)為12.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,某市準(zhǔn)備在道路![]() 的一側(cè)修建一條運(yùn)動(dòng)比賽道,賽道的前一部分為曲線(xiàn)段
的一側(cè)修建一條運(yùn)動(dòng)比賽道,賽道的前一部分為曲線(xiàn)段![]() ,該曲線(xiàn)段是函數(shù)
,該曲線(xiàn)段是函數(shù)![]() ,
, ![]() 時(shí)的圖象,且圖象的最高點(diǎn)為
時(shí)的圖象,且圖象的最高點(diǎn)為![]() .賽道的中間部分為長(zhǎng)
.賽道的中間部分為長(zhǎng)![]() 千米的直線(xiàn)跑道
千米的直線(xiàn)跑道![]() ,且
,且![]() .賽道的后一部分是以
.賽道的后一部分是以![]() 為圓心的一段圓弧
為圓心的一段圓弧![]() .
.

(1)求![]() 的值和
的值和![]() 的大小;
的大小;
(2)若要在圓弧賽道所對(duì)應(yīng)的扇形![]() 區(qū)域內(nèi)建一個(gè)“矩形草坪”,矩形的一邊在道路
區(qū)域內(nèi)建一個(gè)“矩形草坪”,矩形的一邊在道路![]() 上,一個(gè)頂點(diǎn)在半徑
上,一個(gè)頂點(diǎn)在半徑![]() 上,另外一個(gè)頂點(diǎn)
上,另外一個(gè)頂點(diǎn)![]() 在圓弧
在圓弧![]() 上,且
上,且![]() ,求當(dāng)“矩形草坪”的面積取最大值時(shí)
,求當(dāng)“矩形草坪”的面積取最大值時(shí)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】為了得到函數(shù)y=sin3x+cos3x的圖象,可以將函數(shù)y= ![]() cos3x的圖象( )
cos3x的圖象( )
A.向右平移 ![]() 個(gè)單位
個(gè)單位
B.向左平移 ![]() 個(gè)單位
個(gè)單位
C.向右平移 ![]() 個(gè)單位
個(gè)單位
D.向左平移 ![]() 個(gè)單位
個(gè)單位
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
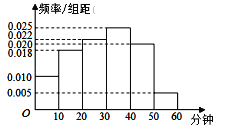
【題目】銀川一中為研究學(xué)生的身體素質(zhì)與課外體育鍛煉時(shí)間的關(guān)系,抽取在校200名學(xué)生的課外體育鍛煉平均每天運(yùn)動(dòng)的時(shí)間(單位:分鐘)進(jìn)行調(diào)查,將收集的數(shù)據(jù)分成![]() ,
,![]() 六組,并作出頻率分布直方圖(如圖),將日均課外體育鍛煉時(shí)間不低于40分鐘的學(xué)生評(píng)價(jià)為“課外體育達(dá)標(biāo)”.
六組,并作出頻率分布直方圖(如圖),將日均課外體育鍛煉時(shí)間不低于40分鐘的學(xué)生評(píng)價(jià)為“課外體育達(dá)標(biāo)”.
課外體育不達(dá)標(biāo) | 課外體育達(dá)標(biāo) | 合計(jì) | |
男 |
| ||
女 |
| ||
合計(jì) |
(1)請(qǐng)根據(jù)直方圖中的數(shù)據(jù)填寫(xiě)下面的![]() 列聯(lián)表,并通過(guò)計(jì)算判斷是否能在犯錯(cuò)誤的概率不超過(guò)
列聯(lián)表,并通過(guò)計(jì)算判斷是否能在犯錯(cuò)誤的概率不超過(guò)![]() 的前提下認(rèn)為“課外體育達(dá)標(biāo)”與性別有關(guān)?
的前提下認(rèn)為“課外體育達(dá)標(biāo)”與性別有關(guān)?
(2)在![]() 這兩組中采取分層抽樣,抽取6人,再?gòu)倪@6名學(xué)生中隨機(jī)抽取2人參加體育知識(shí)問(wèn)卷調(diào)查,求這2人中一人來(lái)自“課外體育達(dá)標(biāo)”和一人來(lái)自“課外體育不達(dá)標(biāo)”的概率.
這兩組中采取分層抽樣,抽取6人,再?gòu)倪@6名學(xué)生中隨機(jī)抽取2人參加體育知識(shí)問(wèn)卷調(diào)查,求這2人中一人來(lái)自“課外體育達(dá)標(biāo)”和一人來(lái)自“課外體育不達(dá)標(biāo)”的概率.
附參考公式與:![]()
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)f(x)=x3+3|x﹣a|(a∈R).
(1)若f(x)在[﹣1,1]上的最大值和最小值分別記為M(a),m(a),求M(a)﹣m(a);
(2)設(shè)b∈R,若[f(x)+b]2≤4對(duì)x∈[﹣1,1]恒成立,求3a+b的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知q和n均為給定的大于1的自然數(shù),設(shè)集合M={0,1,2,…,q﹣1},集合A={x|x=x1+x2q+…+xnqn﹣1 , xi∈M,i=1,2,…n}.
(1)當(dāng)q=2,n=3時(shí),用列舉法表示集合A;
(2)設(shè)s,t∈A,s=a1+a2q+…+anqn﹣1 , t=b1+b2q+…+bnqn﹣1 , 其中ai , bi∈M,i=1,2,…,n.證明:若an<bn , 則s<t.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知橢圓C: ![]() +
+ ![]() =1(a>b>0)的焦距為4,其短軸的兩個(gè)端點(diǎn)與長(zhǎng)軸的一個(gè)端點(diǎn)構(gòu)成正三角形.
=1(a>b>0)的焦距為4,其短軸的兩個(gè)端點(diǎn)與長(zhǎng)軸的一個(gè)端點(diǎn)構(gòu)成正三角形.
(1)求橢圓C的標(biāo)準(zhǔn)方程;
(2)設(shè)F為橢圓C的左焦點(diǎn),T為直線(xiàn)x=﹣3上任意一點(diǎn),過(guò)F作TF的垂線(xiàn)交橢圓C于點(diǎn)P,Q.
①證明:OT平分線(xiàn)段PQ(其中O為坐標(biāo)原點(diǎn));
②當(dāng) ![]() 最小時(shí),求點(diǎn)T的坐標(biāo).
最小時(shí),求點(diǎn)T的坐標(biāo).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com